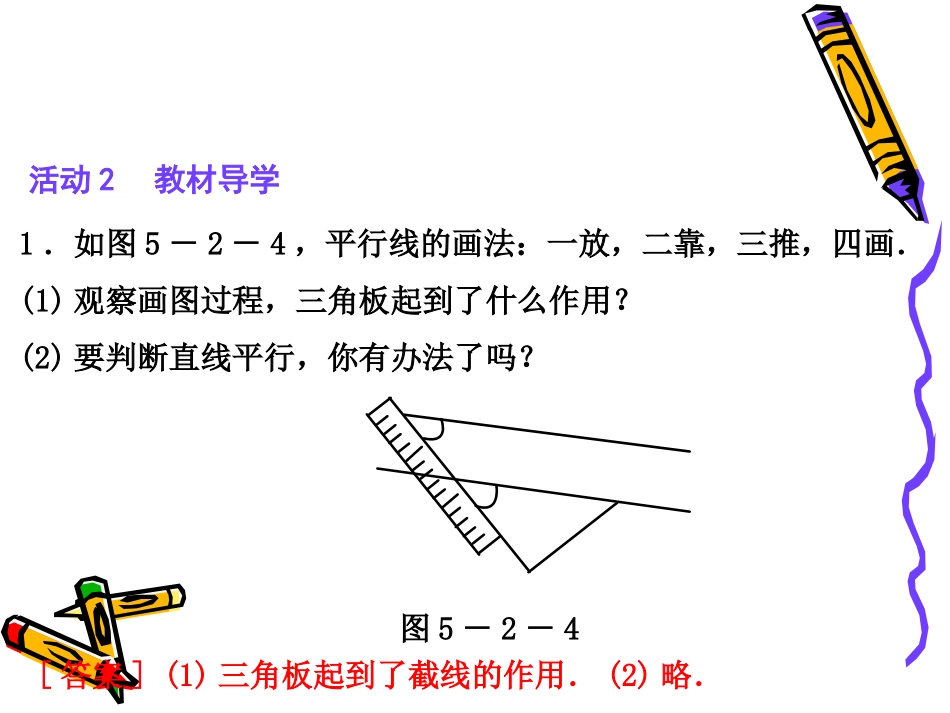
探究新知探究新知重难互动探究重难互动探究新知梳理新知梳理5.2平行线及其判定5.2.2平行线的判定第1课时平行线的判定方法5.2平行线及其判定探究新知活动1知识准备如图5-2-3,直线EF分别交直线AB,CD于点G,H,则图中的同位角有____对,内错角有____对,同旁内角有____对.图5-2-34225.2平行线及其判定活动2教材导学1.如图5-2-4,平行线的画法:一放,二靠,三推,四画.(1)观察画图过程,三角板起到了什么作用?(2)要判断直线平行,你有办法了吗?图5-2-4[答案](1)三角板起到了截线的作用.(2)略.5.2平行线及其判定2.“在同一平面内,垂直于同一条直线的两条直线互相平行”是否可以看做平行线判定方法的特殊情形?如图5-2-5,已知AB⊥CD,AB⊥EF,那么CD∥EF吗?图5-2-5[答案]是CD∥EF5.2平行线及其判定新知梳理知识点平行线的判定方法1:两条直线被第三条直线所截,如果同位角________,那么这两条直线平行.简单说成:同位角________,两直线平行.方法2:两条直线被第三条直线所截,如果内错角________,那么这两条直线平行.简单说成:内错角________,两直线平行.相等相等相等相等5.2平行线及其判定方法3:两条直线被第三条直线所截,如果同旁内角________,那么这两条直线平行.简单说成:同旁内角________,两直线平行.互补互补5.2平行线及其判定例1如图5-2-6.(1)因为∠1=∠A(已知),所以______∥_______();(2)因为∠3=∠4(已知),所以______∥______();(3)因为∠2=∠5(已知),所以______∥______();(4)因为∠ADC+∠C=180°(已知),所以______∥______().图5-2-6BCAD同位角相等,两直线平行ABCD内错角相等,两直线平行ADBC内错角相等,两直线平行ADBC同旁内角互补,两直线平行重难互动探究探究问题一两直线平行的判定方法5.2平行线及其判定[解析](1)要找到∠1和∠A是由直线BC和直线AD被直线AB所截得的同位角,然后根据同位角相等,确定BC和AD平行.(2)要找到∠3和∠4是直线AB和CD被直线BD所截得的内错角.(3)要分清∠2和∠5是直线AD和BC被直线BD所截得的内错角.(4)要知道∠ADC和∠C是直线AD,BC被直线CD所截得的同旁内角.5.2平行线及其判定[归纳总结]同位角相等―→两直线平行内错角相等―→两直线平行同旁内角互补―→两直线平行由角相等或互补关系,判断两直线平行,关键是找出两个角是哪两条直线被哪一条直线所截而成的角.5.2平行线及其判定探究问题二两直线平行的推理例2如图5-2-7,已知AC⊥AE,BD⊥BF,∠1=15°,∠2=15°,AE与BF平行吗?为什么?图5-2-75.2平行线及其判定[解析]要判断AE与BF是否平行,也就是要找同位角相等或内错角相等或同旁内角互补.由题意有∠EAC=∠FBD=90°,∠1=∠2=15°,可得∠EAB=∠FBG=90°+15°=105°.解:平行.理由:因为AC⊥AE,BD⊥BF(已知),所以∠EAC=∠FBD=90°(垂直的定义).因为∠1=∠2(已知),所以∠EAC+∠1=∠FBD+∠2(等式性质),即∠EAB=∠FBG,所以AE∥BF(同位角相等,两直线平行).5.2平行线及其判定例3如图5-2-8所示,直线AB和CD被直线MN所截,EG平分∠BEF,FH平分∠DFE.当∠1与∠2满足什么条件时,AB∥CD?图5-2-85.2平行线及其判定解:当∠1与∠2互余时,AB∥CD.理由:∵EG平分∠BEF,FH平分∠DFE,∴∠BEF=2∠1,∠DFE=2∠2.∵∠1+∠2=90°,∴∠BEF+∠DFE=2(∠1+∠2)=2×90°=180°,所以AB∥CD(同旁内角互补,两直线平行).5.2平行线及其判定[归纳总结]要判断两直线平行,也就是找同位角相等或内错角相等或同旁内角互补.判定两条直线是否平行,方法较多,要灵活运用,不能拘泥于某一种判定方法;另外还要注意同旁内角互补......,而不是相...等.,才可判定两直线平行.