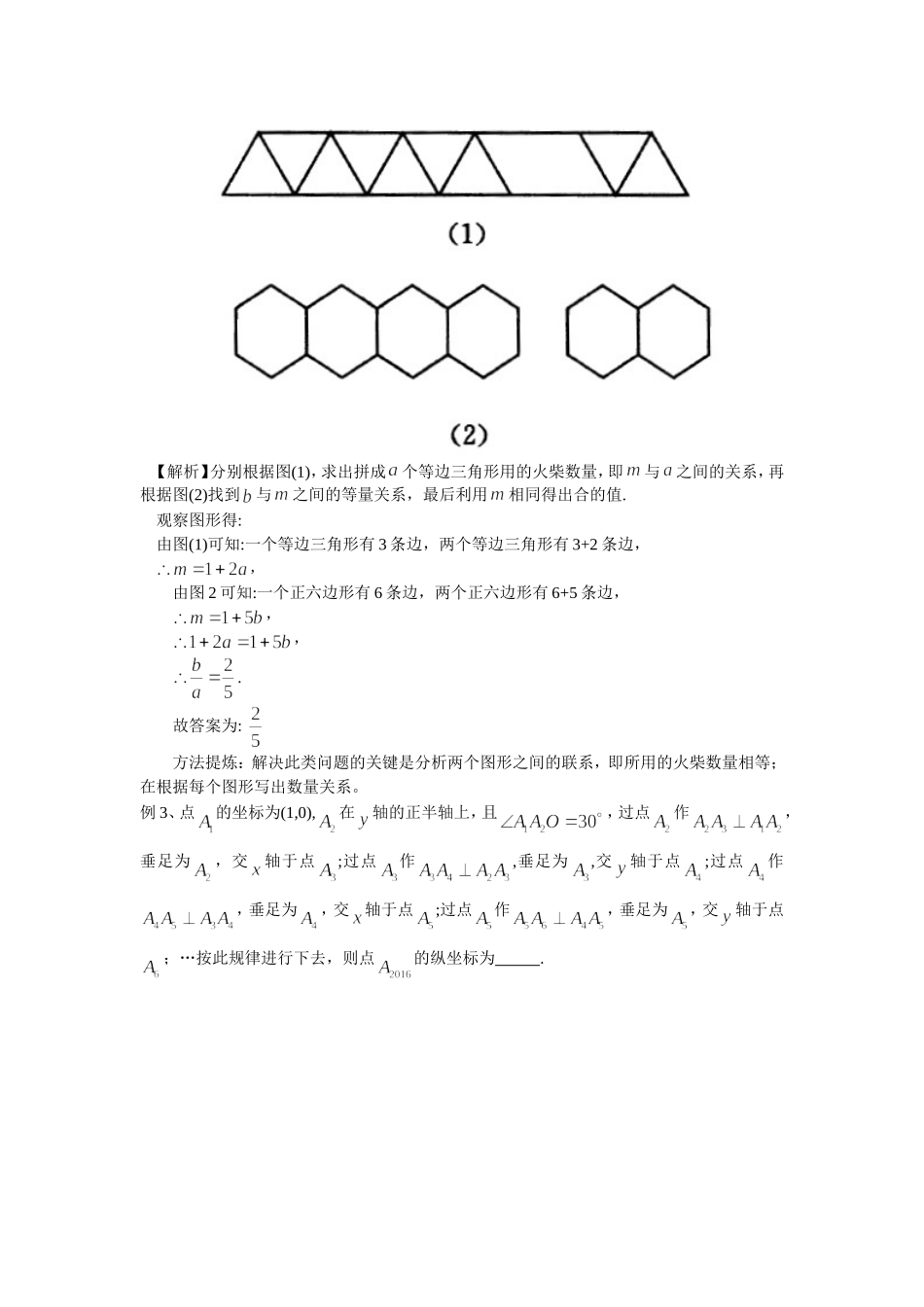
课题:中考复习专题《规律探究问题》安庆四中潘朝晖教学目标1、理解某些数、式、图形及与图形有关的操作、变化过程。2、通过观察、分析、推理探求数、式及图形变化的规律。3、在解决问题的过程中让学生经历观察、归纳、猜想、实验、证明等数学活动,加深对数学知识之间关系的理解。4、进一步理解特殊到一般的数学思想。教学重点:在问题情境背景下应用特殊到一般的数学思想方法。教学流程一、例题讲解例1、一列数…满足条件:且为整数),则=.【解析】:…可以发现:数列以循环出现,2016÷3=672,所以.方法提炼:解决数式规律问题的常用方法:(1)将所给每个数据化为有规律的代数式或等式;(2)按规律排列这些式子;(3)将发现的规律用代数式或等式表示出来;(4)用题中所给的数据验证规律的正确性。例2、用根火柴恰好可拼成如图(1)所示的个等边三角形或如图(2)所示的个正六边形,则=.【解析】分别根据图(1),求出拼成个等边三角形用的火柴数量,即与之间的关系,再根据图(2)找到与之间的等量关系,最后利用相同得出合的值.观察图形得:由图(1)可知:一个等边三角形有3条边,两个等边三角形有3+2条边,,由图2可知:一个正六边形有6条边,两个正六边形有6+5条边,,,.故答案为:方法提炼:解决此类问题的关键是分析两个图形之间的联系,即所用的火柴数量相等;在根据每个图形写出数量关系。例3、点的坐标为(1,0),在轴的正半轴上,且,过点作,垂足为,交轴于点;过点作,垂足为,交轴于点;过点作,垂足为,交轴于点;过点作,垂足为,交轴于点;…按此规律进行下去,则点的纵坐标为.【解析】∵序号除以4整除的话在轴的负半轴上,余数是1在轴的正半轴上,余数是2在轴的正半轴上,余数是3在轴的负半轴上,∵2016÷4=504在轴的负半轴上;只要根据A4、A8的坐标即可求出坐标。故答案为.例4、如图,在平面直角坐标系中,将绕点顺时针旋转到的位置,使点的对应点落在直线上,再将绕点顺时针旋转到的位置,使点的对应点落在直线上,依次进行下去…,若点的坐标是(0,1),点的坐标是(,1),则点的横坐标是.【解析】由题意点的横坐标,点的横坐标,点的横坐标,点的横坐标.故答案为.方法提炼:根据所给的数据和图形从中寻求规律进行解题是解答本类问题的关键。二、练一练1、有一组等式:12+22+22=3222+32+62=7232+42+122=13242+52+202=212请观察它们的构成规律,用你发现的规律写出第8个等式。2、观察下列关于自然数的等式:(1)32-4×12=5(2)52-4×22=9(3)72-4×32=13…根据上述规律解决下列问题:(1)完成第四个等式:92-4×()2=();(2)写出你猜想的第n个等式(用含n的式子表示),并验证其正确性.3、如图,Rt△ABC中,∠ACB=900,AC=2BC=2,作内接正方形A1B1D1C;在Rt△AA1B1中,作内接正方形A2B2D2A1;在Rt△AA2B2中,作内接正方形A3B3D3A2;……;依次作下去,则第n个正方形AnBnDnAn-1的边长是()D1D2B2B3B4B1A4A3A2A1BAC4、已知菱形A1B1C1D1的边长为2,∠A1B1C1=60°,对角线A1C1,B1D1相交于点O.以点O为坐标原点,分别以OA1,OB1所在直线为x轴、y轴,建立如图所示的直角坐标系.以B1D1为对角线作菱形B1C2D1A2∽菱形A1B1C1D1,再以A2C2为对角线作菱形A2B2C2D2∽菱形B1C2D1A2,再以B2D2为对角线作菱形B2C3D2A3∽菱形A2B2C2D2,…按此规律继续作下去,在x轴的正半轴上得到点A1,A2,A3,…,An,则点An的坐标为________.三、小结1、探究规律方法和步骤有哪些?(1)通过对特例(特殊点、特殊数量、特殊线段、特殊位置)的分析,寻找规律并归纳;(2)猜想并写出一般性结论;(3)验证或说明结论是否正确。2、主要用了哪些数学思想方法?特殊到一般