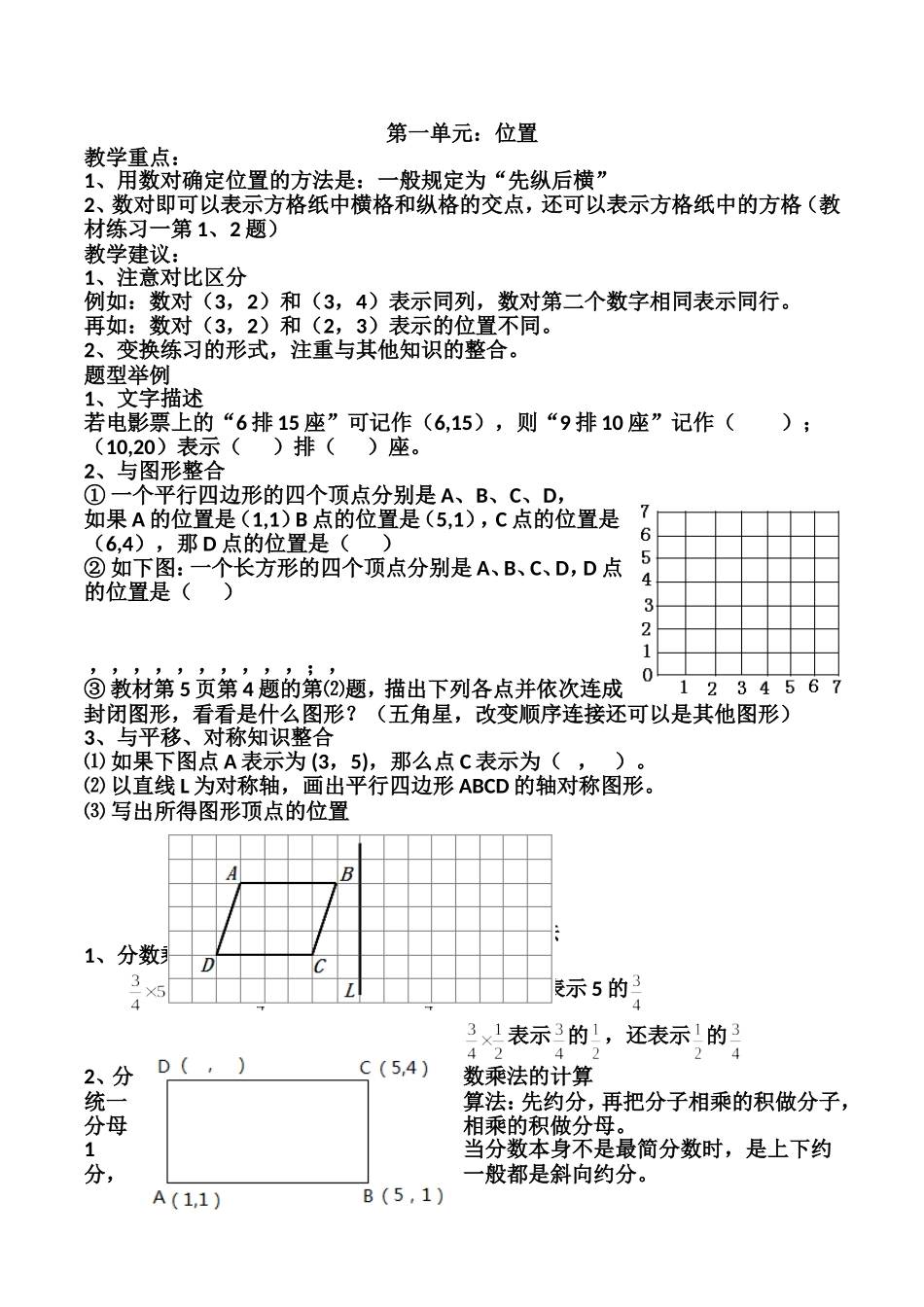
第一单元:位置教学重点:1、用数对确定位置的方法是:一般规定为“先纵后横”2、数对即可以表示方格纸中横格和纵格的交点,还可以表示方格纸中的方格(教材练习一第1、2题)教学建议:1、注意对比区分例如:数对(3,2)和(3,4)表示同列,数对第二个数字相同表示同行。再如:数对(3,2)和(2,3)表示的位置不同。2、变换练习的形式,注重与其他知识的整合。题型举例1、文字描述若电影票上的“6排15座”可记作(6,15),则“9排10座”记作();(10,20)表示()排()座。2、与图形整合①一个平行四边形的四个顶点分别是A、B、C、D,如果A的位置是(1,1)B点的位置是(5,1),C点的位置是(6,4),那D点的位置是()②如下图:一个长方形的四个顶点分别是A、B、C、D,D点的位置是(),,,,,,,,,,;,③教材第5页第4题的第⑵题,描出下列各点并依次连成封闭图形,看看是什么图形?(五角星,改变顺序连接还可以是其他图形)3、与平移、对称知识整合⑴如果下图点A表示为(3,5),那么点C表示为(,)。⑵以直线L为对称轴,画出平行四边形ABCD的轴对称图形。⑶写出所得图形顶点的位置第二单元:分数乘法1、分数乘法的意义表示5个是多少,还表示的5倍,也表示5的表示的,还表示的2、分数乘法的计算统一算法:先约分,再把分子相乘的积做分子,分母相乘的积做分母。1当分数本身不是最简分数时,是上下约分,一般都是斜向约分。例1:例2:2分数乘整数,将整数看做分母是1的分数。例如:3分数乘小数,能直接约分的将小数看做分母是1的分数。例如:4特殊数的计算3、简便运算教材第14页例6:乘法的交换结合律的运用优势不是很明显,重点在分配率的应用。⑴正用:逆用:⑵具有在解决问题中简算的意识,教材第15页练习三第2题,“剪一朵花要用张纸,小明剪了9朵,小红剪了11朵,他们一共用了多少张纸?”4、倒数1倒数是相对于两个数而言的,即使3个数的乘积是1,它们也不是倒数关系。2建议补充:带分数的倒数和小数的倒数。3注意:特殊数0和1的倒数4一个数的倒数一定等于这个数。当时,一个数的倒数一定大于这个数。当时,一个数的倒数一定小于这个数。当时,判断:真分数的倒数是假分数。(√)假分数的倒数是真分数。(×)例如:a、b、c三个数都大于零,当a×1=121×b=×c时,这三个数的大小关系是()。A.b>a>cB.a>b>cC.c>a>bD.b>c>a5、解决问题1数据中含有分数,但数量关系与解答方法与整数相同。速度×时间=路程(第11页例4)单价×时间=总价每份数×份数=总数(第8页例1)工效×时间=工总(第10页例3)以上数量关系可以概括为:单一量×数量=总量⑵由分数乘法的意义扩展而新出现的,求一个数的几分之几是多少的问题。求一个数的几分之几是多少,是具有特殊数量关系的问题,属于两个量相比的关系。教学中要抓住关键的句子,找到两个相比较的量,弄清哪个量是单位“1”,要求的量是单位“1”的几分之几,再根据分数乘法的意义解答。①教学建议:加强线段图的教学,从分数乘法的意义出发,明确数量关系。单位“1”的量×比较量的分率=比较量②题型:稍复杂的,例1:小红有邮票38枚,小华有邮票55枚,小强的邮票数是小红和小华邮票总数的。小强有邮票多少枚?例2:六年级三个班学生帮助图书室修补图书,一班修补了54本,二班修补的是一班的,三班修补的比二班少。三班修补了多少本?区分量率的,例:茶庄原有3kg菊花茶,昨天卖出40%后,今天又卖出kg,还剩多少千克?正确列式是()。A.B.C.D.第三单元:分数除法1、分数除法的意义⑴乘法的逆运算,明确三量之间一乘二除的关系。单一量×数量=总量总量÷数量=单一量(等分)总量÷单一量=数量(包含)例1:将一根绳子的,平均分成8段,每段是这根绳子的几分之几?将一根米长的绳子,平均分成8段,每段绳子长多少米?例2:把L橙汁分装在容器是L的小瓶里,可以装几瓶?⑵教材第30页例3小明小时走了2千米,小红小时走了千米,谁走得快些?比速度,小明走得快比时间,小明走得快2、分数除法的计算⑴分数乘法的法则,分子相乘,分母相乘。除法作为乘法的逆运算,类比为分子相除,分母相除。如:但这种方法有局限性⑵通过...