双曲线及其标准方程(2)VIP免费

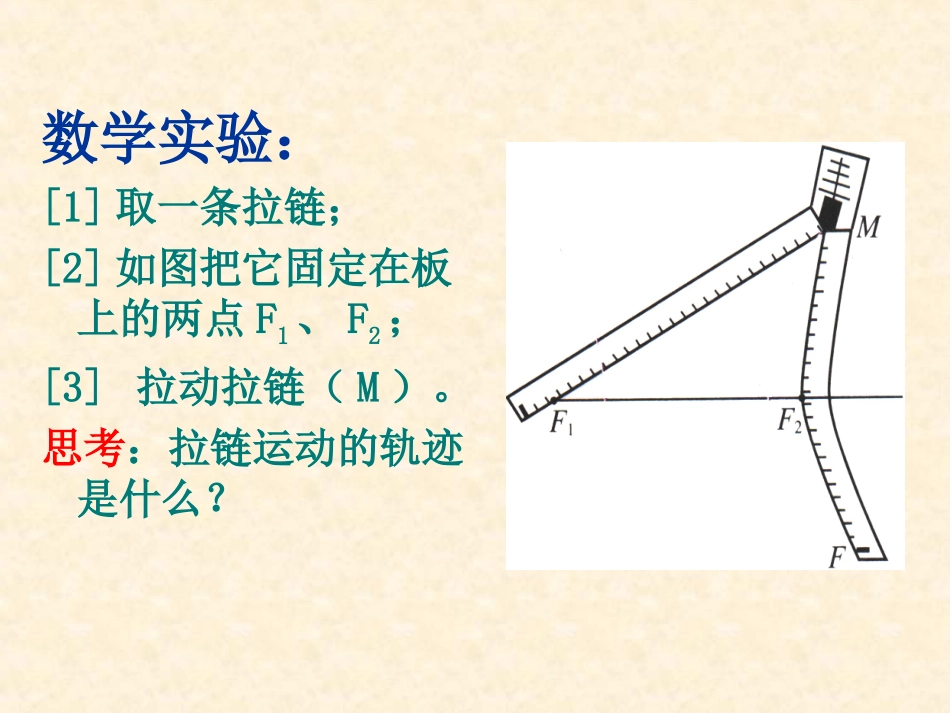
2.2.1双曲线及其标准方程(1)隆德中学【问题1】：椭圆的定义是什么？平面内与两个定点的距离的和等于常数（大于）的点的轨迹叫做椭圆。21,FF21FF【问题2】：如果把上述定义中“距离的和”改为“距离的差”那么点的轨迹会发生怎样的变化？数学实验：[1]取一条拉链；[2]如图把它固定在板上的两点F1、F2；[3]拉动拉链（M）。思考：拉链运动的轨迹是什么？平面内与两定点F1，F2的距离的差的绝对值等于常数2a点的轨迹叫做双曲线。12()FF小于F1,F2---焦点设常数||MF1|-|MF2||=2a|F1F2|---焦距（设为2c）【注意】：对于双曲线定义须抓住三点：1、平面内的动点到两定点的距离之差的绝对值是一个常数；2、这个常数要小于|F1F2|；3、这个常数是非零常数。1F2FMoF2FM1|MF|MF11||--|MF|MF22|=2|=2aa|MF|MF11||--|MF|MF22|=-2|=-2aa||MF||MF11||--|MF|MF22||=2||=2aa（（差的绝对值）差的绝对值）M即双曲线的左支即双曲线的右支即表示整个双曲线【说明】2a12讨论：MFMF12(2).2aFF时，(1).20a时，120MFMF1F2FM1212MFMFFF12MFF的轨迹即为的中垂线12,MFMFM的轨迹即为射线1F2FMM12(3)2aFFM时，的轨迹不存在1、当||MF1|-|MF2||=2a<|F1F2|时，2、当||MF1|-|MF2||=2a=|F1F2|时，3、当||MF1|-|MF2||=2a>|F1F2|时,M点的轨迹不存在4、当||MF1|-|MF2||=2a=0时，M点轨迹是双曲线其中当|MF1|-|MF2|=2a时，M点轨迹是双曲线中靠近F2的一支；当|MF2|-|MF1|=2a时，M点轨迹是双曲线中靠近F1的一支.M点轨迹是在直线F1F2上且以F1和F2为端点向外的两条射线。M点的轨迹是线段F1F2的垂直平分线。结论：如图建立直角坐标系xOy使x轴经过点F1、F2且点O与线段F1、F2的中点重合.设M(x，y)是双曲线上任意一点，|F1F2|=2c，F1(-c,0),F2(c,0),又设点M与F1,F2的距离的差的绝对值等于常数2a.122MFMFa,,222221ycxMFycxMF.22222aycxycx由定义知1F2FMxyO由双曲线定义知,,22acac即022ac因此得令),0(222bbac,222222bayaxb).0,0(12222babyax双曲线的标准方程.说明:1.焦点在x轴;2.焦点F1(-c,0),F2(c,0);4.c2=a2+b2,c最大.).()(22222222acayaxac化简得：1F2FMxyO3.a,b无大小关系;OyxF1F2M双曲线的标准方程双曲线的标准方程1.方程(a>0,b>0)叫做双曲线的标准方程.它所表示的双曲线的焦点在x轴上。12222byax2.方程(a>0,b>0)也是双曲线的标准方程.它所表示的双曲线的焦点在y轴上。12222bxayOF2MxyF1定义图象方程焦点a.b.c的关系1212202MFMFaaFF，22221xyab22221yxab,0Fc0,Fc222cab谁正谁对应a).0,0(12222babxay).0,0(12222babyax双曲线的标准方程：椭圆的标准方程：012222babxay012222babyax2222221.,,aabcccab椭圆中最大在双曲线中最大；相同点：1.,焦点坐标相同焦距相等；2.,,abc焦大小满足勾股定理.不同点：2."",""椭圆方程中双曲线中；3.判断焦点位置方法不同。,ab练习1.根据方程，写出焦点坐标及的值:15151925)1(2222yxyx和143134)2(2222xyyx和3,5),0,4(ba焦点1,15),0,4(ba焦点3,2),0,1(ba焦点2,3),7,0(ba焦点例1、已知双曲线的焦点为F1(-5,0),F2(5,0)，双曲线上一点P到F1、F2的距离的差的绝对值等于6，求双曲线的标准方程.221916xy221169xy221927yx练习1．判断下列方程是否表示双曲线，若是，求出其焦点的坐标.①②③④12422yx12222yx12422yx369422xyF1MF222193xykk说明方程表示的曲线(1)已知双曲线的焦点为F1(0,-5),F2(0,5)，双曲线上一点P到F1、F2的距离的差的绝对值等于6，求双曲线的标准方程.(2)已知双曲线的焦点为F1(0,-5),F2(0,5),双曲线上一点P到F1、F2的距离的差等于6，求双曲线的方程.练习222222222111xyyxabab设或2221xymn设，可避免讨论评:待定系数法曲线的标准方程.,5)的双49(),24求经过两点(3,例2例３221255xy(32,2)求与椭圆共焦点且过点的双曲线的方程.评:１．确定双曲线标...