三角函数图像性质VIP免费

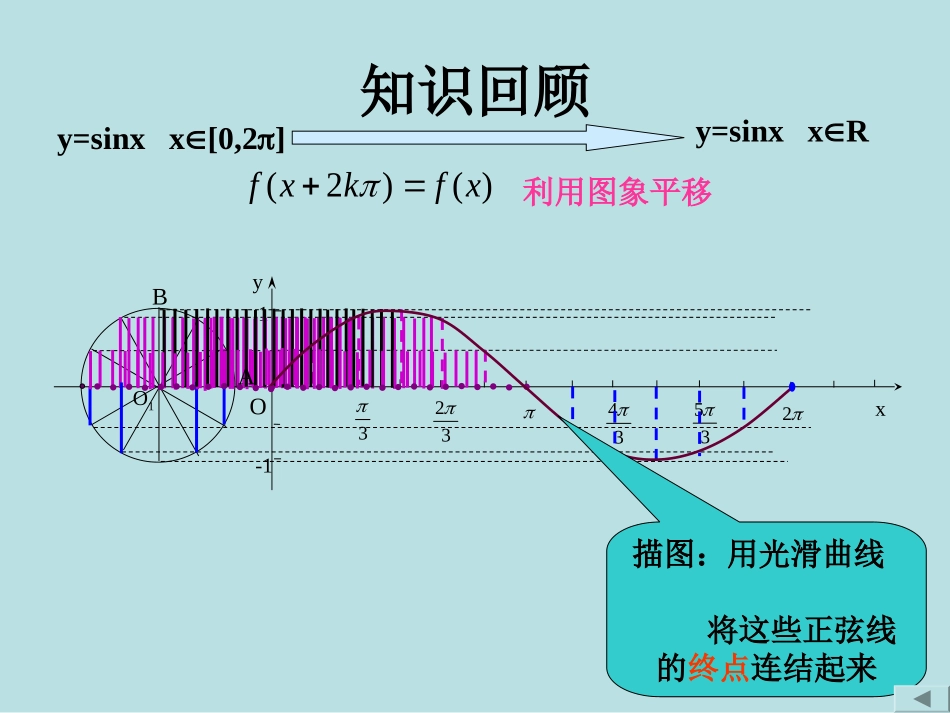
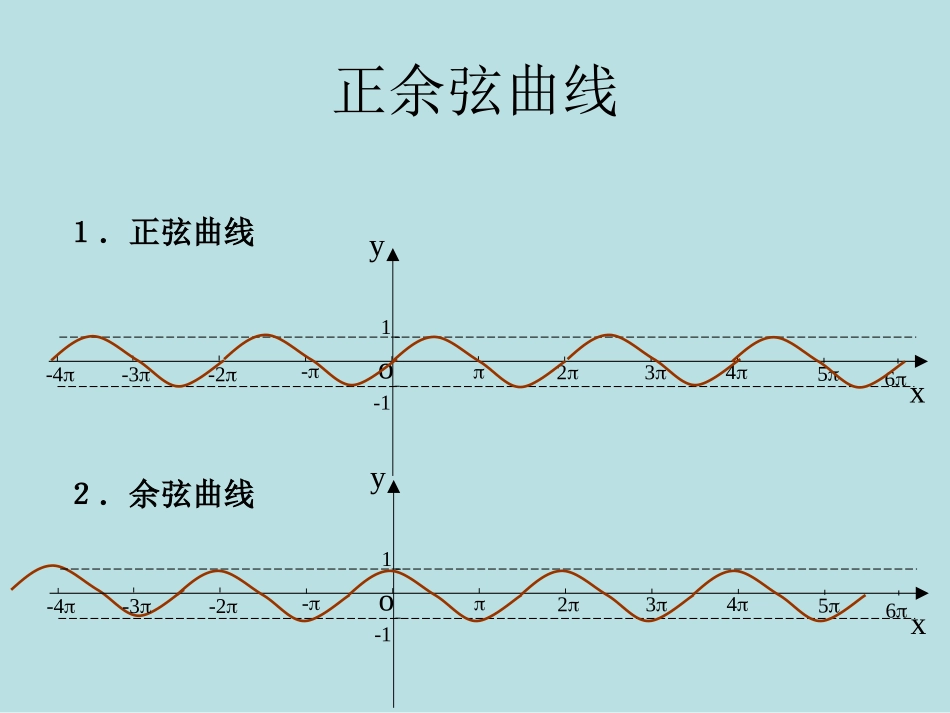
y=sinxx[0,2]O1Oyx33234352-11y=sinxxR)()2(xfkxf描图：用光滑曲线将这些正弦线的终点连结起来利用图象平移AB知识回顾x6yo--12345-2-3-41x6yo--12345-2-3-41１．正弦曲线２．余弦曲线正余弦曲线xy22o22tanyx4.sin()(0,0)yAxA五点法正切曲线y=sinxy=cosxy=tanx{|,}2xxkkZ)(22,22Zkkk)(232,22Zkkk)(2,2Zkkk)(2,2Zkkk)(2,2zkkk))(0,(Zkk)(2Zkkx)(Zkkx))(0,2(Zkk))(0,2(Zkk2T2TT定义域值域奇偶性单调性周期性对称性RRR[-1,1][-1,1]奇函数奇函数偶函数增区间：增区间：增区间：减区间：减区间：对称中心：对称中心：对称中心：对称轴：对称轴：42xxkxkkZ且，2tan1yx的定义域。有关正切函数定义域的定义域是1sin2)1(xy的奇偶性是xxysin)2(的最小正周期是xy3tan2)3((4)sin(2),8yxx函数图象的一条对称轴是直线基础训练Zkkk652,623T偶函数Zkk,4五种题型题型一：三角函数周期性题型二：三角函数值域与最值题型三：三角函数单调性题型四：y=Asin(ωx+φ)图象题型五：综合应用1.一般地，对于函数f(x),如果存在一个非零的常数T，使得定义域内的每一个x的值，都满足f(x+T)=f(x)，那么函数f(x)就叫做周期函数周期函数非零常数T叫做这个函数的周期周期2.对于一个周期函数f(x),如果在它所有的周期中存在一个最小的正数，那么这个最小的正数就叫做f(x)的最小正周最小正周期。期。题型一：周期性一般地，函数y=Asin(ωx+φ)及y=Acos(ωx+φ)（其中A,ω,φ为常数，且A≠0,ω≠0）的周期是:三角函数周期求法：2(0)T函数y=Atan(ωx+φ)(A≠0,ω≠0)周期为T1。定义法2。公式法1sincos12sinsin23sincosyxxyxyxyxx（）（）（）22T2TT2T求下列函数周期例：若钟摆的高度h(mm)与时间t(s)之间的函数关系如图所示：(1)求该函数的周期;(2)求t=10s时钟摆的高度123th60555045403530252015105123456789o105020周期应用f(10)=f(1+6×1.5)=f(1)=20,cos(2)06331,yaxbab变式：已知函数的定义域是，，值域为，，试确定的值。cos(2)(0,)63yxx求函数的值域。题型二：求三角函数的值域和最值（例1）2,0cos(2)1,[01]6626xx值域为，01403334011aabaabbabaabb时显然不成立时时3sin1cos2xyx例2。求函数的最大、小值。2223sincos213sin2121sinsin1321210210133321021033xyxyyxyyxxyyyy解：，（）（），（）即，得从而得最小值，最大值题型三：三角函数的单调性tancot,33例1。若、（，）且则必有()２（Ａ）（Ｂ）（C）(D)２２33tantan2223tan2232yx解：变形为：（）又，（，）在（，）为增函数，则3sin4433sin2222352222242445[22]44yuuxuxyukukkxkkxkkkkZ法一：由，复合而成，是减函数，则即需递减，，即，得--递增区间为-，-，sin43372222242443722]44yxkxkkxkkkkZ法二：化为（），即需，递增区间为[，，3sin()4yx求的单调递增区间。例2cos2044,,33tan336,46xkxkknZxnxnxkxkkZ解：即定义域为232tan3tanlgcos2yxxx求定义域例3求y=f(x)的解析式例1．函数y=Asin(ωx+φ)的图象在y轴右侧的第一个最高点...