数学、九年级下册、263实际问题与二次函数（1）VIP免费

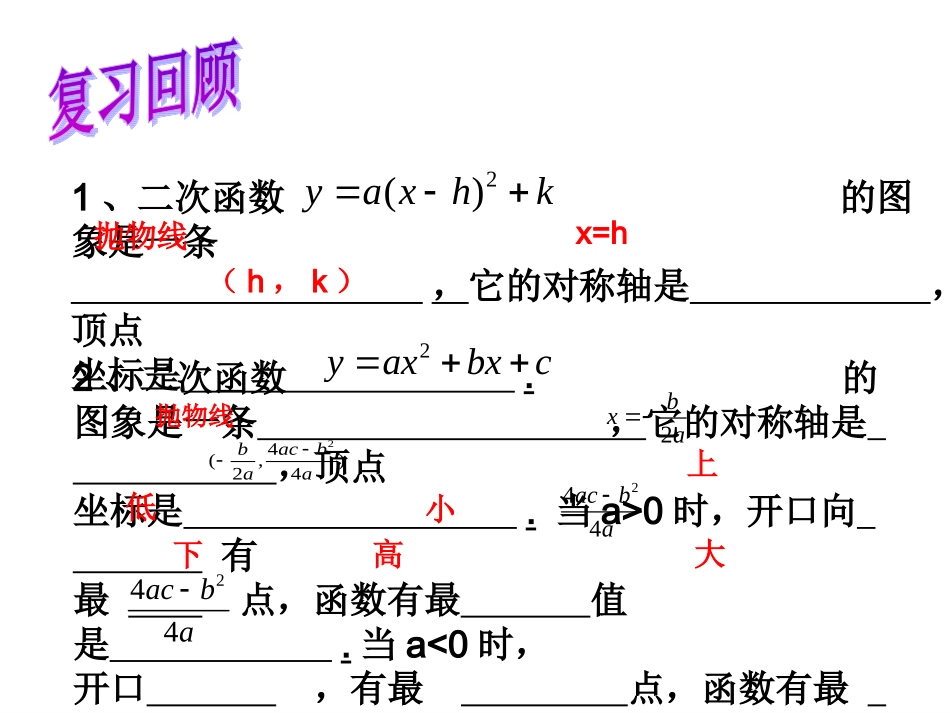
生活是数学的源泉，我们是数学学习的主人1、二次函数的图象是一条，它的对称轴是，顶点坐标是.2()yaxhk抛物线x=h（h，k）2、二次函数的图象是一条，它的对称轴是，顶点坐标是.当a>0时，开口向有最点，函数有最值是.当a<0时，开口，有最点，函数有最值，是.2bxa2yaxbxc抛物线24(,)24bacbaa244acba244acba上低小下高大3、二次函数的对称轴是,顶点坐标是，当x=时，y的最值是.2289yxx4、关于销售问题的一些等量关系.（单件商品）利润=售价—进价总利润=单件商品利润×销售量x=2(2,1)2小1知识准备：某商品成本为20元，售价为30元，卖出200件，则利润为元，①若价格上涨x元，则利润为元；②若价格下降x元，则利润为元；③若价格每上涨1元，销售量减少10件，现价格上涨x元，则销售量为件，利润为元；④若价格每下降1元，销售量增加20件，现价格下降x元，则销售量为件，利润为元；2000200（10+x）200（10-x）（200-10x）(10+x)(200-10x)(200+20x)(10-x)(200+20x)在日常生活中存在着许许多多的与数学知识有关的实际问题。如繁华的商业城中很多人在买卖东西。如果你去买商品，你会选买哪一家的？如果你是商场经理，如何定价才能使商场获得最大利润呢？问题：某商品现在的售价为每件60元，每星期可卖出300件，市场调查反映：每涨价1元，每星期少卖出10件；每降价1元，每星期可多卖出20件，已知商品的进价为每件40元，如何定价才能使利润最大？涨价：（1）设每件涨价x元，则每星期售出商品的利润y也随之变化，我们先来确定y与x的函数关系式。涨价x元时则每星期少卖_____件，实际卖出___________件,销额为_______________元，买进商品需付________________元因此，所得利润为_____________________________元即6000100102xxy625060005100510522最大值时，yabx所以，当定价为65元时，利润最大，最大利润为6250元元\x元\y625060005300(0≤x≤30)10x(300-10x)40(300-10x)(60+x)(300-10x)y=(60+x)(300-10x)-40(300-10x)解：设降价x元时利润最大，则每星期可多卖20x件，实际卖出（300+20x)件，销售额为(60-x)(300+20x)元，买进商品需付40(300-10x)元，因此，得利润61256000256025182522最大时，当yabx答：定价为元时，利润最大，最大利润为6125元2157600010020203004020300602xxxxxy(0≤x≤20)（1）列出二次函数的解析式，并根据自变量的实际意义，确定自变量的取值范围；（2）在自变量的取值范围内，运用公式法或通过配方求出二次函数的最大值或最小值。练一练1.科技园电脑销售部经市场调查发现，销售某型号电脑所获利润y(元)与销售台数x（台）满足,则当卖出()台时，所获利润最大。16000202xy202.已知某人卖盒饭x（个）与所获利润y（元）满足关系式，则这人可获得的最大利润是()35760012002xxy24003.童装专卖店销售一种曲奇牌的童装，已知这种童装每天所获利润y（元）与童装的销售单价x（元）满足关系式则要想获得每天的最大利润，必须以销售单价（）元售出。500502xxy254.某商店购进一批单价为20元的日用商品，如果以单价30元销售，那么半月内可售出400件，根据销售经验，提高销售单价会导致销售量减少，即销售单价每提高1元，销售量相应减少20件，设销售单价增加x元（x≥30）,那么（1）销售量可以表示为（）件，销售单价（），所获得利润可以表示为（）元（2）当销售单价是（）元时，可以获得最大利润，最大利润是（）元。5.已知某产品的销售利润y（元）与单价x(元)之间满足关系式，则为了最大利润，其单价应定为（）54002400102xy400－20x30+x45005202xy3545001206.某商店经营一种小商品，进价为每件20元，据市场分析，在一月内，售价为每件25元时，可卖出105件，而售价每上涨1元，则少卖5件，则当售价定为30元时，一个月可获利（）元。8007.某商店购进一批单价为20元的日用品,如果以单价30元销售,那么半个月内可以售出400件.根据销售经验,提高单价会导致销售量的减少,即销售单价每提高1元,销售量相应减少20件.售...