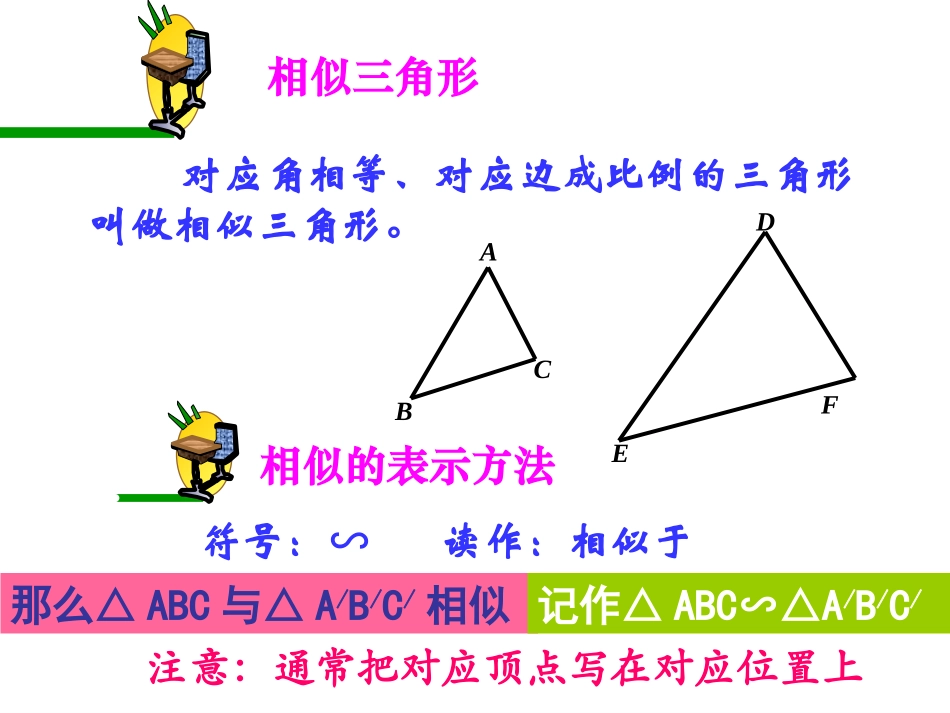
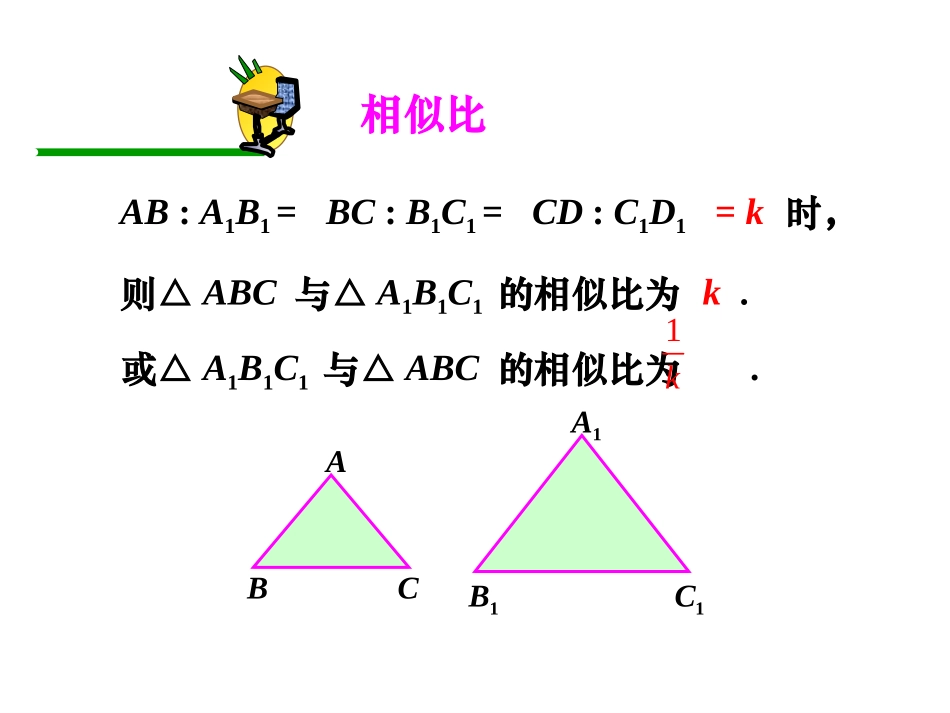
相似三角形的性质杨秀志相似三角形对应角相等、对应边成比例的三角形叫做相似三角形。ABCEDF相似的表示方法符号:∽读作:相似于那么△ABC与△A/B/C/相似记作△ABC∽△A/B/C/注意:通常把对应顶点写在对应位置上相似比AB:A1B1=BC:B1C1=CD:C1D1=k时,ABCA1B1C1则△ABC与△A1B1C1的相似比为k.或△A1B1C1与△ABC的相似比为.1kABCDEF如图,ΔABC∽ΔDFE则它们的对应角分别是则它们的对应角分别是∠∠AA与∠与∠_____,_____,∠∠BB与∠与∠__________,,∠∠CC与∠与∠__________;;对应边成比例的是对应边成比例的是DFEABACBCDFDEFE已知:DE//BC,且D是边AB的中点,DE交AC于E.猜想:△ADE与△ABC有什么关系?并证明。ABCDE证明:且∠A=A∠∵DE//BC∴∠1=B∠,∠2=C∠∴△ADE与△ABC的对应角相等相似。12三角形的中位线截得的三角形与原三角形相似,相似比。∴四边形DBFE是平行四边形∴DE=BF,DB=EF∴△ADE∽ABC△ABCDEF过E作EF//AB交BC于F又∵DE//BC又∵AD=DB∴AD=EF∵∠A=3∠,∠2=C∠∴△ADEEFC△∴DE=FC=BF,∴∴∴△ADE与△ABC的对应边成比例23AE=EC12AEAC12DEBC12ADAEDEABACBC12已知:DE//BC,△ADE与△ABC有什么关系?猜想:△ADE与△ABC有什么关系?相似。ABCDEF当点D在AB上任意一点时,上面的结论还成立吗?12你能证明吗?平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似。知识要点知识要点平行于三角形一边的定理ABCDE即:在△ABC中,如果DEBC∥,那么△ADEABC∽△A型你还能画出其他图形吗?ABCDE即:在△ABC中,如果DEBC∥,那么,ADAEDEABACBC,ADAEDBEC,DBECADAE,ABACBCADAEDE(上比全,全比上)(上比下,下比上)(下比全,全比下)DBECABAC,,ABACDBECABCDE相似具有传递性△ADEABC∽△MN如果再作MN∥DE,共有多少对相似三角形?△AMNADE∽△△AMNABC∽△共有三对相似三角形。请写出它们的对应边的比例式请写出它们的对应边的比例式训练3.已知:如图,AB∥EF∥CD,CDABEFO3图中共有____对相似三角形。△EOFCOD∽△ABEF∥△AOBFOE∽△ABCD∥EFCD∥△AOBDOC∽△4.如图,在△ABC中,DGEHFIBC∥∥∥,(1)请找出图中所有的相似三角形;(2)如果AD=1,DB=3,那么DG:BC=_____。ABCDEFGHI△ADGAEHAFIABC∽△∽△∽△1:45.如图,DEBC∥交AB于D,交AC于E,若AD:DB=2:3,BC=15,求DE的长。ADBEC教学反思