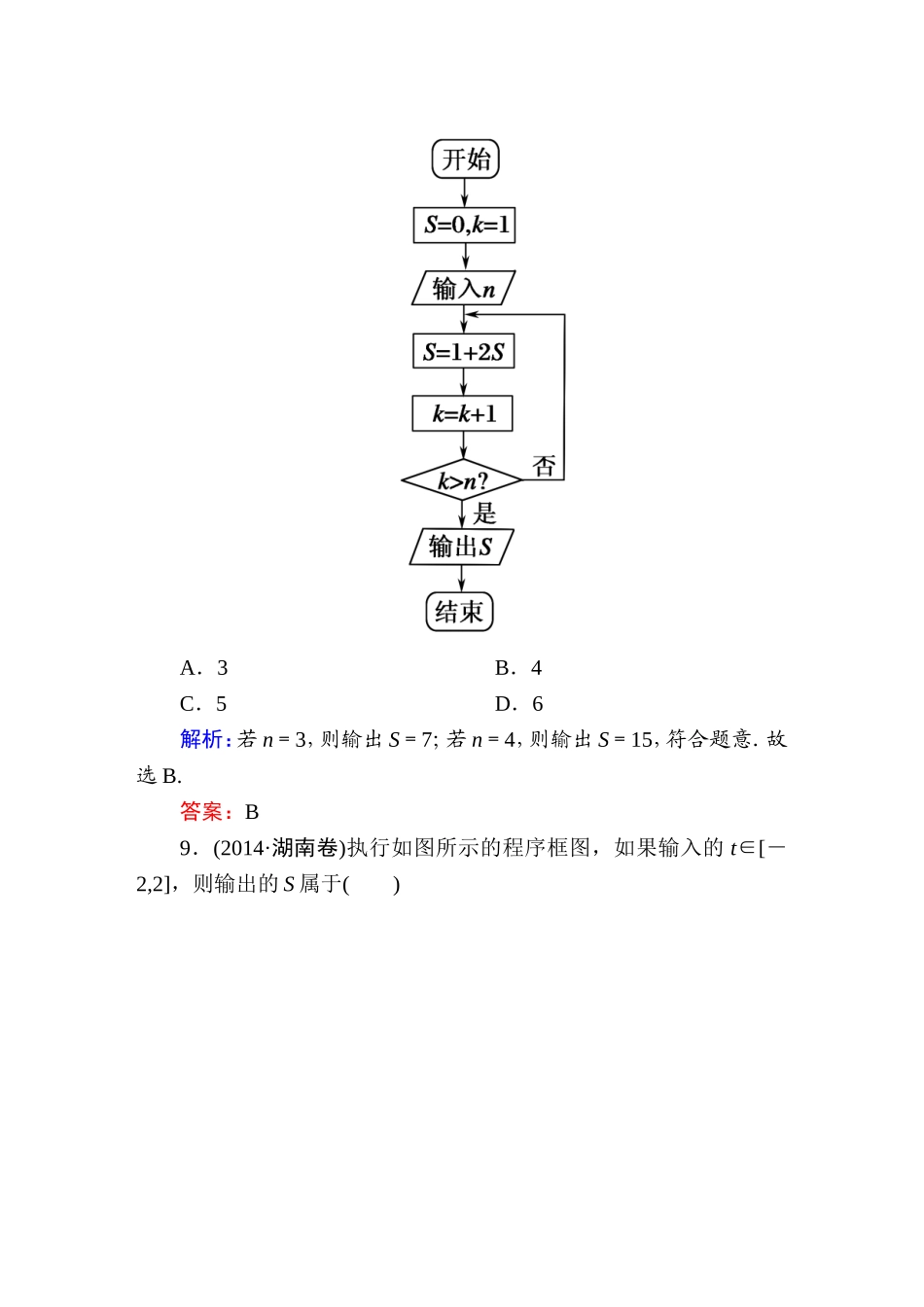
课时作业2平面向量、复数、算法初步时间:45分钟一、选择题1.(2014·山东卷)已知a,b∈R,i是虚数单位,若a-i与2+bi互为共轭复数,则(a+bi)2=()A.5-4iB.5+4iC.3-4iD.3+4i解析:由已知得,a=2,b=1,即a+bi=2+i,所以(a+bi)2=(2+i)2=3+4i,选D.答案:D2.(2014·新课标卷Ⅰ)=()A.1+iB.1-iC.-1+iD.-1-i解析:==-1-i,故选D.答案:D3.(2014·安徽卷)设i是虚数单位,表示复数z的共轭复数.若z=1+i,则+i·=()A.-2B.-2iC.2D.2i解析:+i=+i(1-i)=1-i+i+1=2.答案:C4.(2014·福建卷)在下列向量组中,可以把向量a=(3,2)表示出来的是()A.e1=(0,0),e2=(1,2)B.e1=(-1,2),e2=(5,-2)C.e1=(3,5),e2=(6,10)D.e1=(2,-3),e2=(-2,3)解析:由题意知,A选项中e1=0,C、D选项中两向量均共线,都不符合基底条件,故选B(事实上,a=(3,2)=2e1+e2).答案:B5.(2014·大纲卷)若向量a、b满足:|a|=1,(a+b)⊥a,(2a+b)⊥b,则|b|=()A.2B.C.1D.解析:由题意得:(a+b)·a=0,(2a+b)·b=0,即a·b+a2=0,2a·b+b2=0,又|a|=1,∴a·b=-1,从而b2=2,∴|b|=.答案:B6.(2014·四川卷)平面向量a=(1,2),b=(4,2),c=ma+b(m∈R),且c与a的夹角等于c与b的夹角,则m=()A.-2B.-1C.1D.2解析:由题意得:=⇒=⇒=⇒m=2,选D.答案:D7.在△ABC中,AB=2,AC=3,AB·BC=1,则BC=()A.B.C.2D.解析: AB·BC=1,且AB=2,∴1=|AB||BC|cos(π-B),∴|BC|cosB=-.在△ABC中,|AC|2=|AB|2+|BC|2-2|AB||BC|·cosB,即9=4+|BC|2-2×2×.∴|BC|=.答案:A8.阅读如图所示的程序框图,运行相应的程序.如果输入某个正整数n后,输出的S∈(10,20),那么n的值为()A.3B.4C.5D.6解析:若n=3,则输出S=7;若n=4,则输出S=15,符合题意.故选B.答案:B9.(2014·湖南卷)执行如图所示的程序框图,如果输入的t∈[-2,2],则输出的S属于()A.[-6,-2]B.[-5,-1]C.[-4,5]D.[-3,6]解析:由程序框图知,当0≤t≤2时,输出S=t-3,此时S∈[-3,-1];当-2≤t<0时,执行t=2t2+1后1|a-b|,此时,|a+b|2>|a|2+|b|2;当a,b夹角为钝角时,|a+b|<|a-b|,此时,|a-b|2>|a|2+|b|2;当a⊥b时,|a+b|2=|a-b|2=|a|2+|b|2,故选D.答案:D二、填空题13.(2014·江苏卷)已知复数z=(5+2i)2(i为虚数单位),则z的实部为________.解析:由题意z=(5+2i)2=25+2×5×2i+(2i)2=21+20i,其实部为21.答案:2114.(2014·四川卷)复数=________.解析:==-2i.答案:-2i15.(2014·北京卷)复数()2=________.解析:复数===i,故()2=i2=-1.答案:-116.(2014·辽宁卷)执行如图所示的程序框...