立体几何中的向量方法VIP免费

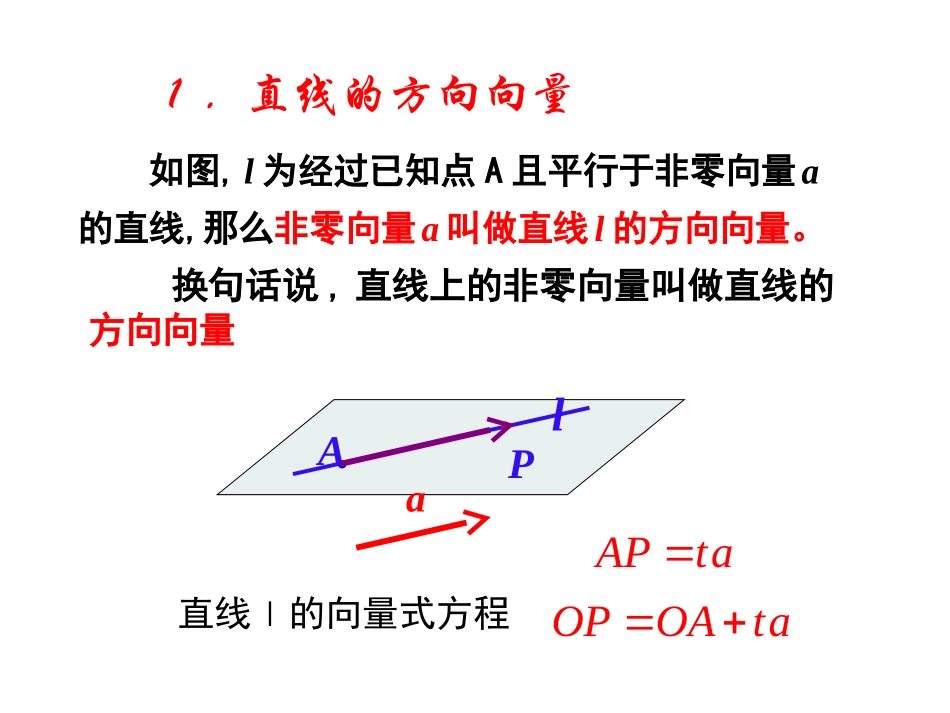
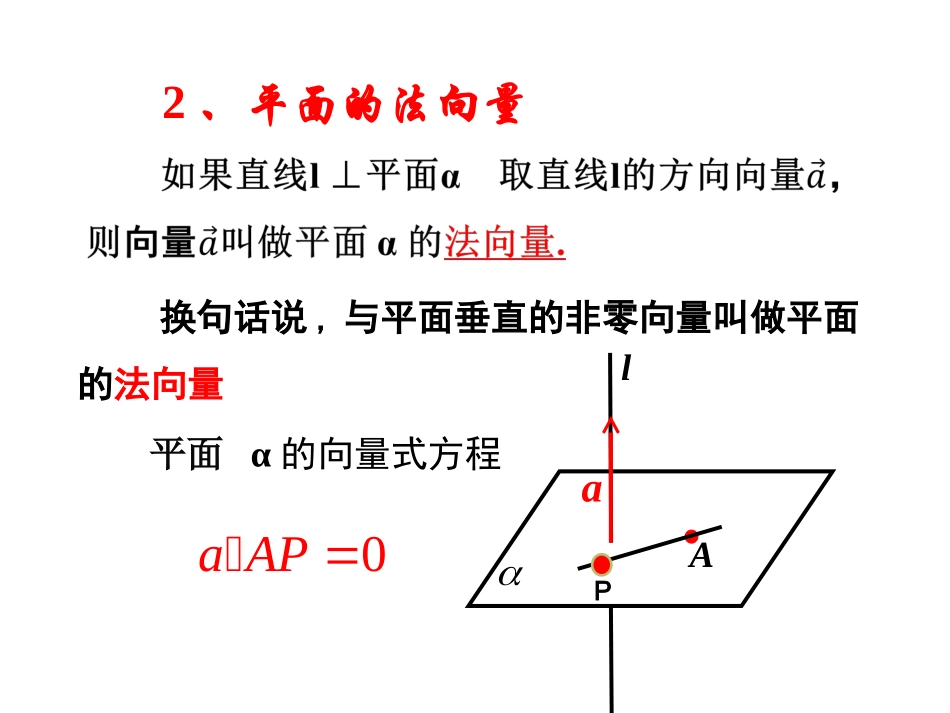
3.2.1立体几何中的向量方法——方向向量与法向量如图,l为经过已知点A且平行于非零向量a的直线,那么非零向量a叫做直线l的方向向量。lAPa１．直线的方向向量直线ｌ的向量式方程OPOAta�换句话说,直线上的非零向量叫做直线的方向向量APta�2、平面的法向量AalP平面α的向量式方程0aAP��换句话说,与平面垂直的非零向量叫做平面的法向量oxyzABCO1A1B1C1练习如图所示,正方体的棱长为1(1)直线OA的一个方向向量坐标为___________(2)平面OABC的一个法向量坐标为___________(3)平面AB1C的一个法向量坐标为___________(-1,-1,1)(0,0,1)(1,0,0)练习.在空间直角坐标系内,设平面经过点，平面的法向量为，为平面内任意一点，求满足的关系式。),,(000zyxP),,(CBAe),,(zyxMzyx,,000(,,)PMxxyyzz�，解：由题意可得0PMe000(,,)(,,)0ABCxxyyzz即000()()()0AxxByyCzz化简得：由两个三元一次方程组成的方程组的解是不惟一的，为方便起见，取z=1较合理。其实平面的法向量不是惟一的。(2,2,1),(4,5,3),ABACABC�例：已知求平面的单位法向量。nxyz解：设平面的法向量为（，，），(2,2,1)0(4,5,3)0,nABnACxyzxyz��则，（，，），（，，）220,4530xyzxyz即1121xzy取，得1(,1,1),2n3||2n122(-333ABC平面的单位法向量为，，）练习如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC=1,E是PC的中点，求平面EDB的一个法向量.ABCDPE解：如图所示建立空间直角坐标系.(0,0,0),(0,0,1),11(0,,)22PE依题意得DB(1,1，0)11(0,,)22DE��DB=(1,1，0)XYZ设平面EDB的法向量为(,,1)nxy,nnDEDB��则1101,1,1220ynxy于是定理一个平面内的两条相交直线与另一个平面平行,则这两个平面平行已知直线l与m相交,,,lm,lm∥∥.求证∥l,ma,,.bv��证明取的方向向量取,的法向量u,lm∥∥,avbvvuαβab,,b又a不共线所以v是的一个法向量于是v同时是、的一个法向量.∥ｌｍ设直线l,m的方向向量分别为,ab，平面,的法向量分别为,uv，则(1)//lm//abab；mlab3.平行关系：(2)//l①au0au；3.平行关系：aaAC��②∥axAByAD��③设直线l,m的方向向量分别为,ab，平面,的法向量分别为,uv，则uα3.平行关系：v(3)//①//uv.uvuαβ设直线l,m的方向向量分别为,ab，平面,的法向量分别为,uv，则u②巩固性训练设分别是平面α,β的法向量,根据下列条件,判断α,β的位置关系.vu,)4,1,3(),5,3,2()3()4,4,2(),2,2,1()2()4,4,6(),5,2,2()1(vuvuvu垂直平行相交作业P1041(1)(2)2(1)(2)