相似三角形复习VIP免费

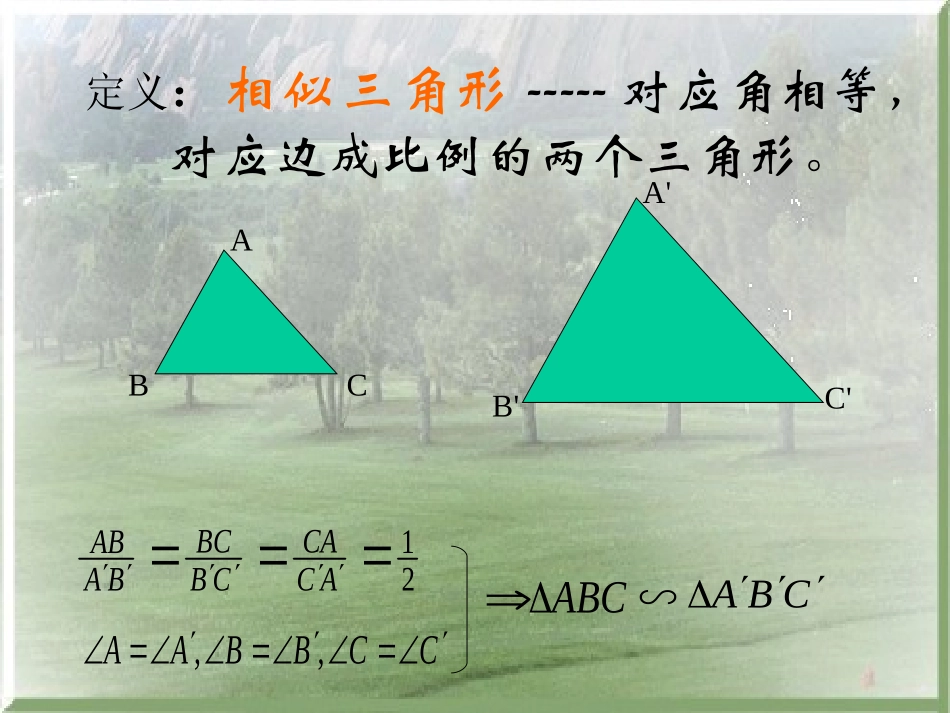
初三数学相似三角形判定复习课•指导思想：充分发挥学生的主体作用，提高有意注意强度，启迪学生思维，发展学生能力。•内容分析：相似三角形是初中数学中一个重要内容，在各种题型中如何灵活运用也是一个难点之一。掌握好此块内容，对整个初中数学有着举足轻重的作用。•教学目标：让同学明确判定两三角形相似的几种方法，理清证明相似的思路并熟练掌握、灵活应用，在练习中掌握证明相似技巧。•教学重点：证明两个三角形相似的四种方法。•教学难点：选择何种方法来证明相似，即方法的灵活使用。初三数学“相似三角形判定”复习课定义：相似三角形-----对应角相等，对应边成比例的两个三角形。21ACCACBBCBAABCCBBAA,,ABCCBA∽ABCA'B'C'简言之：平行得相似ABCDEABCDE情况1：DE与两边相交DE//BC=>∽ABCADE情况2：DE与两边延长线相交DE//BC=>∽ABCADE相似判定方法一：平行于三角形一边的直线和其他两边（或两边的延长线相交），所构成的三角形与原三角形相似。简言之：两对应边成比例且夹角相等得相似ABCA'B'C'CBBCBAABBBABCCBA∽相似判定方法二:如果一个三角形的两条边和另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似。简言之：两角相等得相似ABCCBA∽AABBA'B'C'ABC相似判定方法三：如果一个三角形的两个角和另一个三角形的两个角对应相等，那么这两个三角形相似。简言之：三边对应成比例得相似ABCA'B'C'ACCACBBCBAABABCCBA∽相似判定方法四：如果一个三角形的三条边和另一个三角形的三条边对应成比例，那么这两个三角形相似。解题思路再证夹角相等用方法2或看第三组边用方法4再证一对应角相等方法3或找夹此对应角的两组边对应成比例用方法2（1）若有平行线--------先考虑用方法1（2）若可找到两组边成比例---（3）若已有一对应角相等--总结-------要证明两个三角形相似的方法有：方法1：平行得相似方法2：两边成比例且夹角相等得相似方法3：两角相等得相似方法4：三边对应成比例得相似ACDB例1：在△ABC中，D是AC上一点，要使△ABD∽ACB△至少还需的条件是________________.例1：在△ABC中，D是AC上一点，要使△ABD∽ACB△至少还需的条件是________________.ABADACABACDB分析：对△ABD和△ACB而言，已有一公共角A，因此对照前面的解题思路3：先找另一角证相等或找夹此角的两边对应成比例。这样分析，本题答案已很清楚，为ABD=ACB，或ADB=ABC或ACBE练习：对上题稍作改动：过AB边上一点E画直线，与三角形另一边相交，使所构成的三角形与原三角形相似，这样的直线能画几条？ACBED答案：4条DEBCAED=CDEACBDE=ADACBEACBEDDACBE例2：已知如图梯形ABCD中，ABCD，A=DBC，AB=a，BD=b，DC=c，求证：方程ax2-2bx+c=0有两个相等实数根。ADCBabcADCB21abc证明：AB//CD1=2又A=DBCBCD∽ADBDC/DB=BD/AB即c/b=b/ab2-ac=0而对于方程ax2-2bx+c=0其判别式=4b2-4ac利用上述结论知=0故原方程有两个相等实数根。例2：已知如图梯形ABCD中，ABCD，A=DBC，AB=a，BD=b，DC=c，求证：方程ax2-2bx+c=0有两个相等实数根。例3：如图在ABC中AB=AC，AD垂直BC于点D，E、F在AD上，且AF=FE=ED=BD=CD，求证：BEF∽AEBABFEDCABFEDC分析：要证BEF和AEB相似，现有的条件是有一个公共钝角，接下来思路是再证找一组角相等或找两边成比例，显然由已知条件可以知道应该证明夹这个钝角的两组对应边EF，BE和BE，AE成比例。若设AF=FE=ED=BD=CD=a这样，AE=2a，而BE可用勾股定理求得，从而以边的比值相等来证成比例。例3：如图在ABC中AB=AC，AD垂直BC于点D，E、F在AD上，且AF=FE=ED=BD=CD，求证：BEF∽AEBABFEDC又BEF=AEBBEF∽AEBCEAEBEEFaaAEBEaaBEEFaBE22222222而证明：由已知，设AF=FE=ED=BD=CD=a，则AE=2a,在BED中由勾股定理得，例4：如图ABC是等边三角形，DAE=120°，求证：BC2=BD·CEADBCEADBCE21例4：...