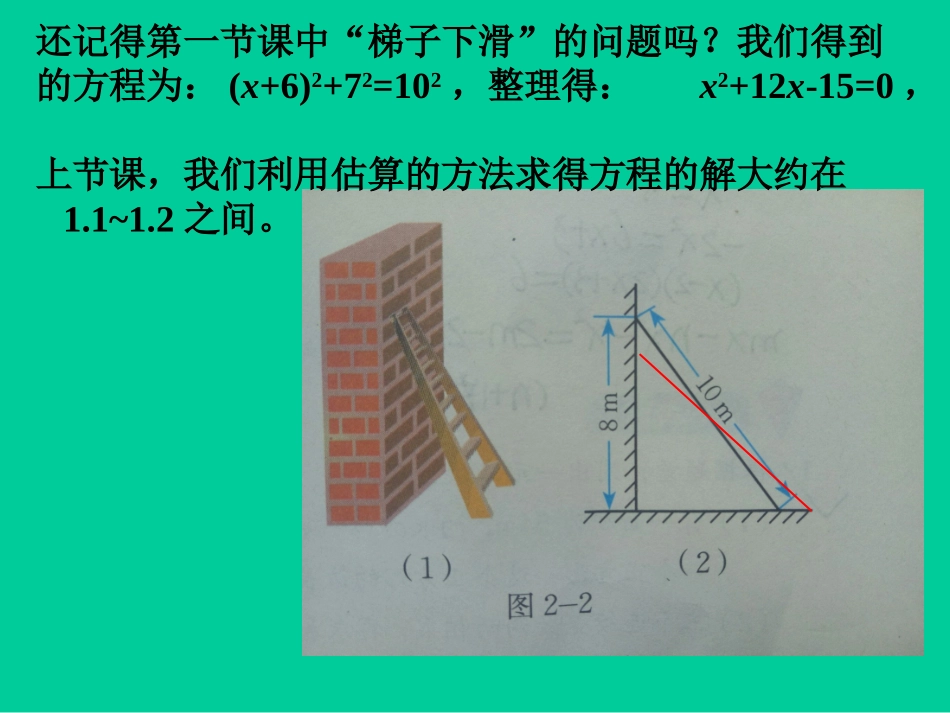
还记得第一节课中“梯子下滑”的问题吗?我们得到的方程为:(x+6)2+72=102,整理得:x2+12x-15=0,上节课,我们利用估算的方法求得方程的解大约在1.1~1.2之间。第二章一元二次方程——用配方法求解一元二次方程(一)沙峁九年制学校高鹏霞1.会用直接开平方法解形如(x+m)2=n(n≥0)的方程;2.理解配方法,会用配方法解二次项系数为1的一元二次方程x2+px+q=0;3.经历将一元二次方程x2+px+q=0转化为:(x+m)2=n(n≥0)的形式的过程,体会转化的数学思想。学习目标挑战自我解下列一元二次方程:1.x2=252.(x-1)2=16直接开平方整体思想:把x-1看成一个整体,然后直接开平方像这样,利用平方根的定义,在方程两边同时开平方,求解一元二次方程的方法,叫做直接开平方法。一元二次方程解法?形如x2=a,(a≥0)的方程,其解为X=±√a形如(x+m)2=n,(n≥0)的方程,其解为X=-m±√n1、直接开平方法.1、直接开平方法.一元二次x2+12x-15=0能直接开平方?.2;2)()(222222babababaabab因式分解的完全平方公式x2+8x+=()2x2+42x+4a2+2ab+b2=(a+b)24+42配方依据:完全平方公式.a2±2ab+b2=(a±b)22x填上适当的数组成完全平方式总结规律:对于x2+px,添上一次项系数一半的平方,就能配一个含未知数的完全平方式。即+()²练习:填上适当的数组成完全平方式x2+12x+____=(x)²x2-4x+____=(x)²x2+8x+____=(x)²y2+6x+____=(y)²6²4²2²3²+6-2+4+3移项两边加上62,使左边配成完全平方式左边写成完全平方的形式开平方,降次或变成了(x+m)2=n21215xx222126156xx2(6)51x651x651x651x12:651,651xx得212150xx像这样,通过配方,把方程左边化成一个完全平方式,然后两边直接开平方,得到一元二次方程的根,这种求解一元二次方程的方法叫配方法。用配方法解一元二次方程的一般步骤有:1.(移)项——使方程左边为二次项和一次项,右边为常数项;2.(配)方——方程两边都加上一次项系数一半的平方,使原方程变为(x+m)2=n的形式;3.(开)方——如果方程右边是非负数,即n≥0,就可左右两边开平方得x+m=4.(解)两个一次方程,得到原方程的根。n前面“梯子下滑”的问题中的方程为:(x+6)2+72=102,整理得:x2+12x-15=0解:移项,得:x2+12x=15,配方,得:x2+12x+62=15+36,即:(x+6)2=51开方,得:但因为x表示梯子底部滑动的距离,所以,不合题意舍去。答:梯子底部滑动的距离是米。∴注意:遇到实际问题,一定要验证根的合理性。2-6-510x12-6+51-6-51xx,6+51解下列方程:(3)x2-14x+50=0;(4)x2+2x+2=8x+4.(1)x2-10x+25=7;(2)x2+3x=10;用开平方法解一元二次方程一种是直接开平方法,一种是配方法。1形如x2=n,(n≥0)方程直接开平方法X=±√n2形如(x+m)2=n,(n≥0)方程,用直接平方法得+mX=±√n3形如x2+px+q=0的一元一次方程用配方法转化为(x+m)2=n,(n≥0)的形式.小结:+()²作业1.课本37页习题2.3:①第1题、第2题②选做第3题.2.试着思考二次项系数不为1的一元二次方程如何解?