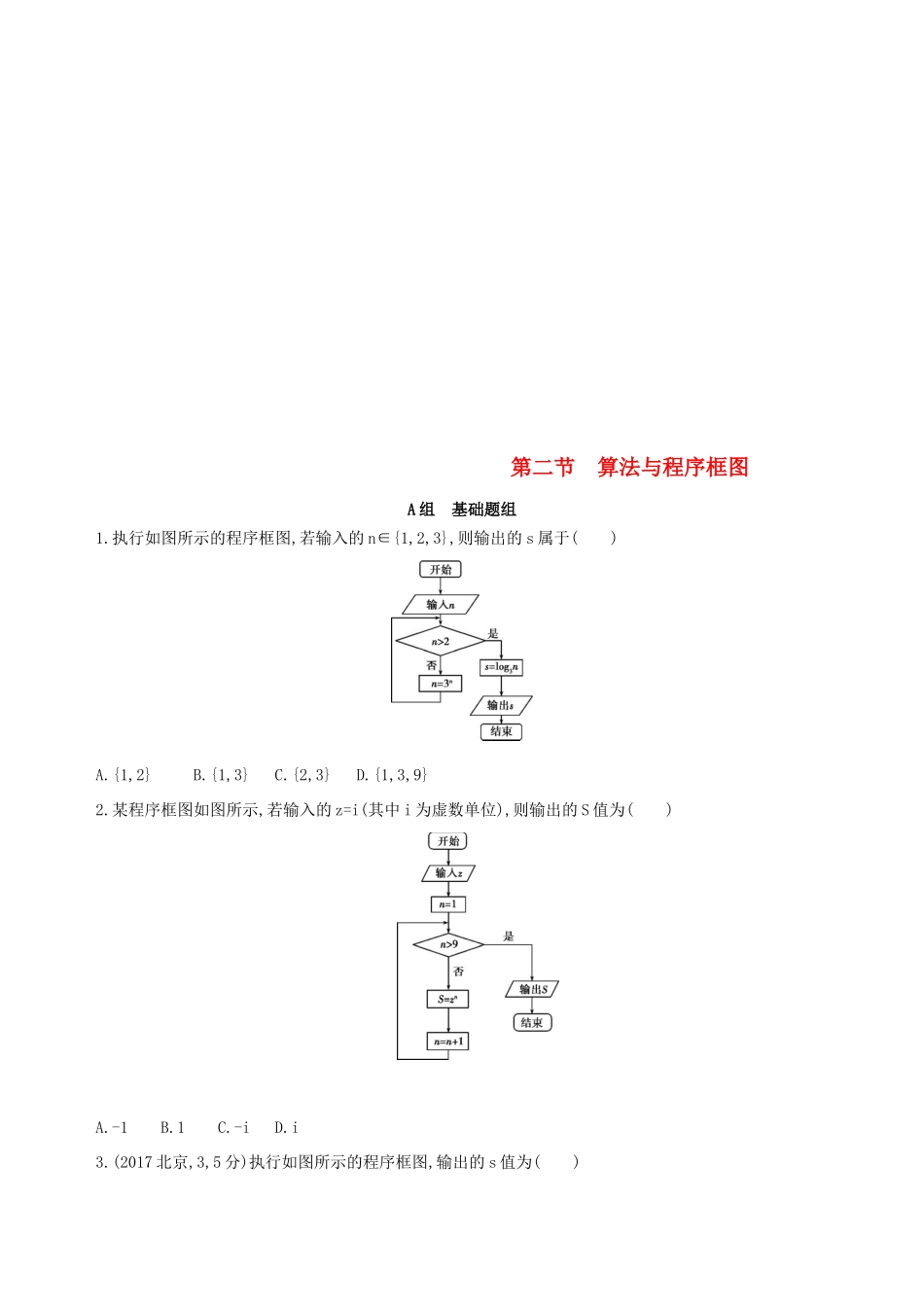
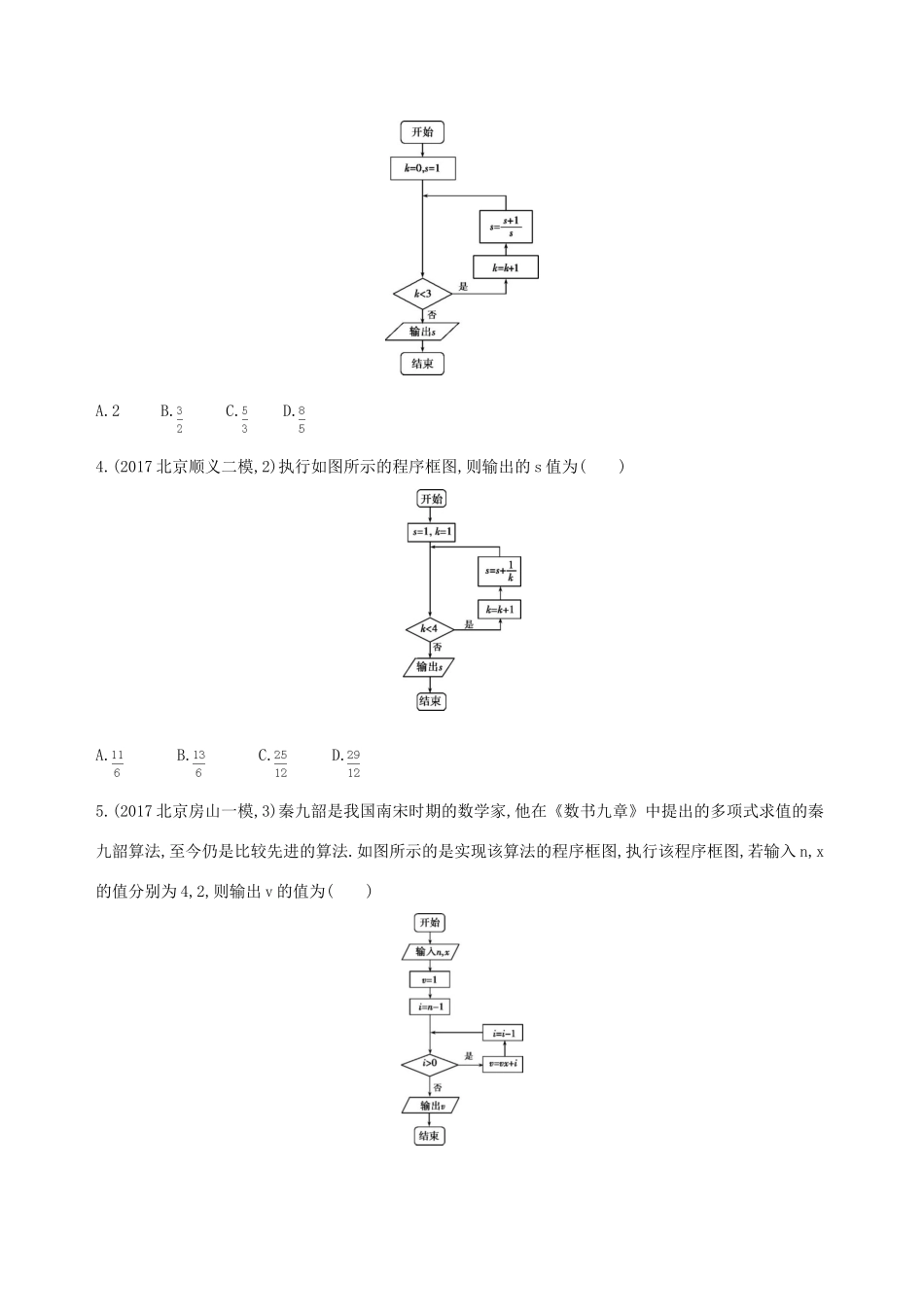
第二节算法与程序框图A组基础题组1.执行如图所示的程序框图,若输入的n∈{1,2,3},则输出的s属于()A.{1,2}B.{1,3}C.{2,3}D.{1,3,9}2.某程序框图如图所示,若输入的z=i(其中i为虚数单位),则输出的S值为()A.-1B.1C.-iD.i3.(2017北京,3,5分)执行如图所示的程序框图,输出的s值为()A.2B.C.D.4.(2017北京顺义二模,2)执行如图所示的程序框图,则输出的s值为()A.B.C.D.5.(2017北京房山一模,3)秦九韶是我国南宋时期的数学家,他在《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的是实现该算法的程序框图,执行该程序框图,若输入n,x的值分别为4,2,则输出v的值为()A.5B.12C.25D.50B组提升题组6.(2015北京,3,5分)执行如图所示的程序框图,输出的结果为()A.(-2,2)B.(-4,0)C.(-4,-4)D.(0,-8)7.(2017北京海淀零模,3)执行如图所示的程序框图,则输出的S值为()A.1B.3C.7D.158.(2017北京西城二模,9)执行如图所示的程序框图,输出的S值为.9.(2017北京丰台二模,10)执行如图所示的程序框图,若输入x的值为6,则输出x的值为.答案精解精析A组基础题组1.A当n=1时,s=log33=1;当n=2时,s=log39=2;当n=3时,s=log33=1,所以输出的s属于{1,2},故选A.2.D条件n>9,则n=10时跳出循环,故n的最大值为9,S=z9=i9=i8·i=i.3.C由程序框图可知k=1,s=2;k=2,s=;k=3,s=.此时k<3不成立,故输出s=.故选C.4.Ck=1,s=1,1<4,进入循环;k=2,s=,2<4,进入循环;k=3,s=,3<4,进入循环;k=4,s=,4=4,输出s=,故选C.5.Cn=4,x=2,v=1,i=3,3>0,循环;v=2×1+3=5,i=2,2>0,循环;v=2×5+2=12,i=1,1>0,循环;v=2×12+1=25,i=0,0=0,输出v=25.故选C.B组提升题组6.B第一次进入循环体:s=0,t=2,x=0,y=2,k=1<3;第二次进入循环体:s=-2,t=2,x=-2,y=2,k=2<3;第三次进入循环体:s=-4,t=0,x=-4,y=0,k=3,满足k≥3,循环结束,此时输出(x,y)为(-4,0),故选B.7.D由程序框图可知S=0+20+21+22+23=15,故选D.8.答案7解析开始:S=1,i=1;第一次循环:S=1+21=3,i=1+1=2;第二次循环:S=3+22=7,i=2+1=3,此时跳出循环,输出S=7.9.答案0解析第1次循环:y=4,x=4,不满足x≤1;第2次循环:y=2,x=2,不满足x≤1;第3次循环:y=0,x=0,满足x≤1,故输出x=0.