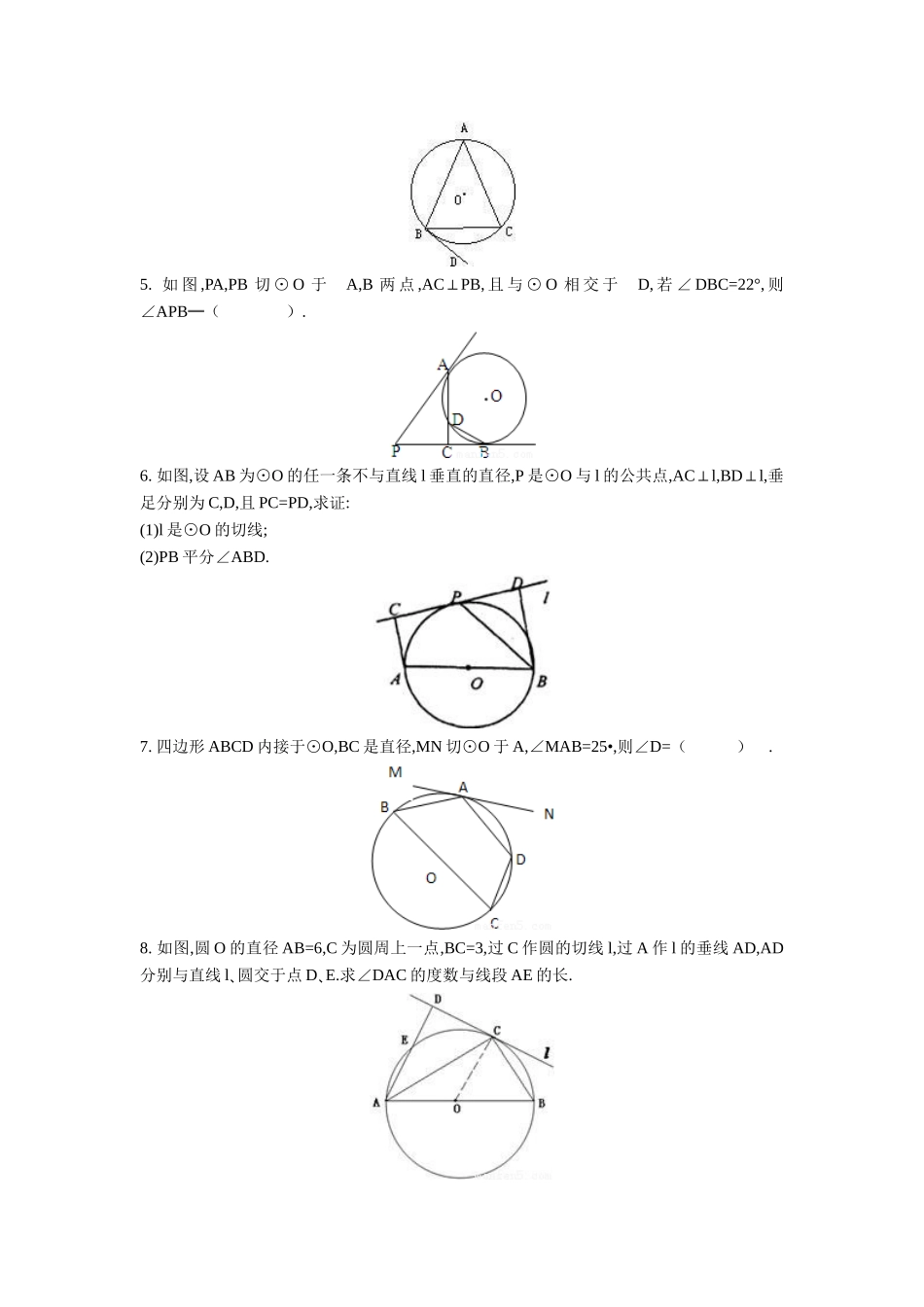
《2.4弦切角的性质》同步练习51.如图:△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,BE∥MN交AC于点E,若AB=6,BC=4,则AE的长为()A.B.C.D.2.如图,圆M与圆N交于A,B两点,以A为切点作两圆的切线分别交圆M和圆N于C,D两点,延长DB交圆M于点E,延长CB交圆N于点F.已知BC=5,DB=10.(1)求AB的长;(2)求3.圆O是三角形ABC的外接圆,过点C的切线交AB的延长线于点D,CD=2,AB=BC=3,则AC的长为()。4.如图,△ABC内接于⊙O,BD切⊙O于点B,AB=AC,若∠CBD=40°,则∠ABC等于________.5.如图,PA,PB切⊙O于A,B两点,AC⊥PB,且与⊙O相交于D,若∠DBC=22°,则∠APB═().6.如图,设AB为⊙O的任一条不与直线l垂直的直径,P是⊙O与l的公共点,AC⊥l,BD⊥l,垂足分别为C,D,且PC=PD,求证:(1)l是⊙O的切线;(2)PB平分∠ABD.7.四边形ABCD内接于⊙O,BC是直径,MN切⊙O于A,∠MAB=25•,则∠D=().8.如图,圆O的直径AB=6,C为圆周上一点,BC=3,过C作圆的切线l,过A作l的垂线AD,AD分别与直线l圆交于点、D、E.求∠DAC的度数与线段AE的长.9.如图,在⊙O中,AB是弦,AC是⊙O切线,过B点作BD⊥AC于D,BD交⊙O于E点,若AE平分∠BAD,则∠ABD的度数是()A.30°B.45°C.50°D.60°10.△ABC内接于⊙O,BD切⊙O于点B,AB=AC,若∠CBD=40°,则∠ABC等于________.《2.4弦切角的性质》同步练习5答案1.A2.(1)(2)13.4.70°5.44°6.证明:(1)连接OP,因为AC⊥l,BD⊥l,所以AC∥BD.又OA=OB,PC=PD,所以OP∥BD,从而OP⊥l.因为P在⊙O上,所以l是⊙O的切线.(2)连接AP,因为l是⊙O的切线,所以∠BPD=∠BAP.又∠BPD+∠PBD=90°,∠BAP+∠PBA=90°,所以∠PBA=∠PBD,即PB平分∠ABD.7.115°8.∠DAC=20°AE=39.A10.70°