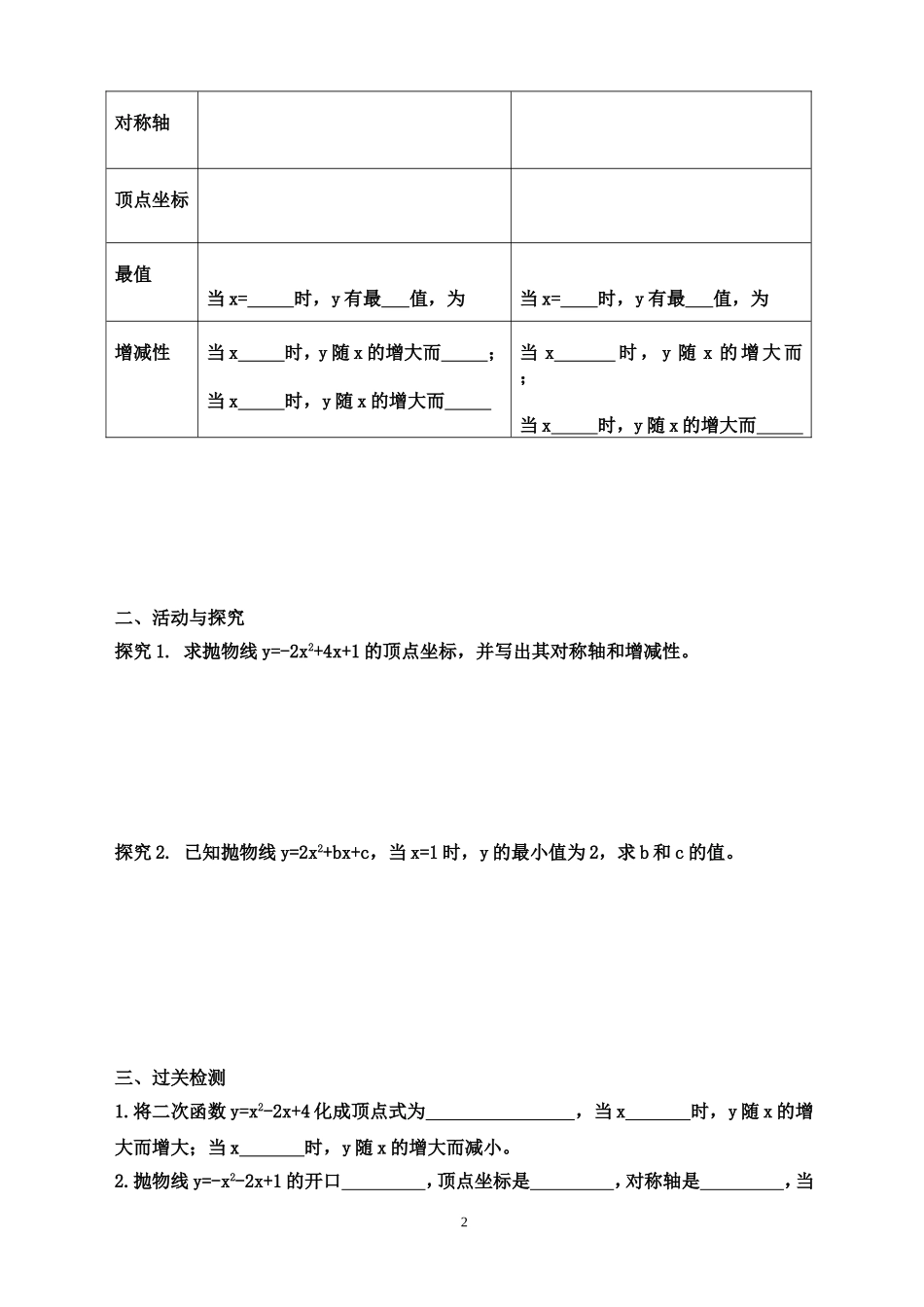
二次函数y=ax2+bx+c(a≠0)的图象与性质学习目标:1.会用配方法确定抛物线y=ax2+bx+c(a≠0)的对称轴、顶点坐标和最值。2.会用顶点坐标公式确定抛物线y=ax2+bx+c(a≠0)的对称轴、顶点坐标和最值。3.掌握二次函数y=ax2+bx+c(a≠0)的图象及性质。学习重(难)点:1.会确定抛物线y=ax2+bx+c(a≠0)的对称轴、顶点坐标和最值。2.掌握二次函数y=ax2+bx+c(a≠0)的图象及性质。学习过程一、自学指导1、复习旧知:①抛物线y=a(x-h)2+k(a≠0)的顶点坐标是,对称轴是。②把抛物线y=-6x2向上平移3个单位,再向左平移5个单位得到抛物线的解析式为,它的顶点是,对称轴是,当x时,y随x的增大而增大。当x时,y随x的增大而减小;当x=时,y有最值,值为。③填空:x2+6x+=(x+)2;2x2-4x+=(x-)22、自主学习:(1)●做一做:(我自信,我最棒!)用配方法把二次函数化成顶点式。●想一想:(我尝试,我成功!)你能说出它的顶点、对称轴、最值、增减性吗?(2)用配方法把二次函数一般式y=ax2+bx+c(a≠0)化为顶点式。●归纳:抛物线y=ax2+bx+c(a≠0)的性质:抛物线y=ax2+bx+c(a>0)y=ax2+bx+c(a<0)开口方向对称轴顶点坐标最值当x=时,y有最值,为当x=时,y有最值,为增减性当x时,y随x的增大而;当x时,y随x的增大而当x时,y随x的增大而;当x时,y随x的增大而二、活动与探究探究1.求抛物线y=-2x2+4x+1的顶点坐标,并写出其对称轴和增减性。探究2.已知抛物线y=2x2+bx+c,当x=1时,y的最小值为2,求b和c的值。三、过关检测1.将二次函数y=x2-2x+4化成顶点式为,当x时,y随x的增大而增大;当x时,y随x的增大而减小。2.抛物线y=-x2-2x+1的开口,顶点坐标是,对称轴是,当2x=时,y有最值,其值为。3.已知抛物线y=-x2+2x+c2的对称轴与x轴交于点(m,n),则m=..4.当a<0时,判断抛物线y=x2+2ax+1+2a2的顶点在第几象限。四、学习体会五、作业设计1.导学2.已知点(2,5)、(4,5)是抛物线y=ax2+bx+c(a≠0)上的两点,则这条抛物线的对称轴为。3.已知:抛物线y=-x2+(3-k)x+2k-1与y轴的交点位于点(0,5)的上方,则k的取值范围是。4.已知二次函数y=x2-x+m.①写出图象的开口方向,对称轴及顶点坐标。②当m为何值时,顶点在x轴上方。③若抛物线与y轴交于点A,过点A作AB∥x轴交抛物线于点B。当三角形ABO面积为4时,求该二次函数解析式。3