等比数列求和(2)VIP免费

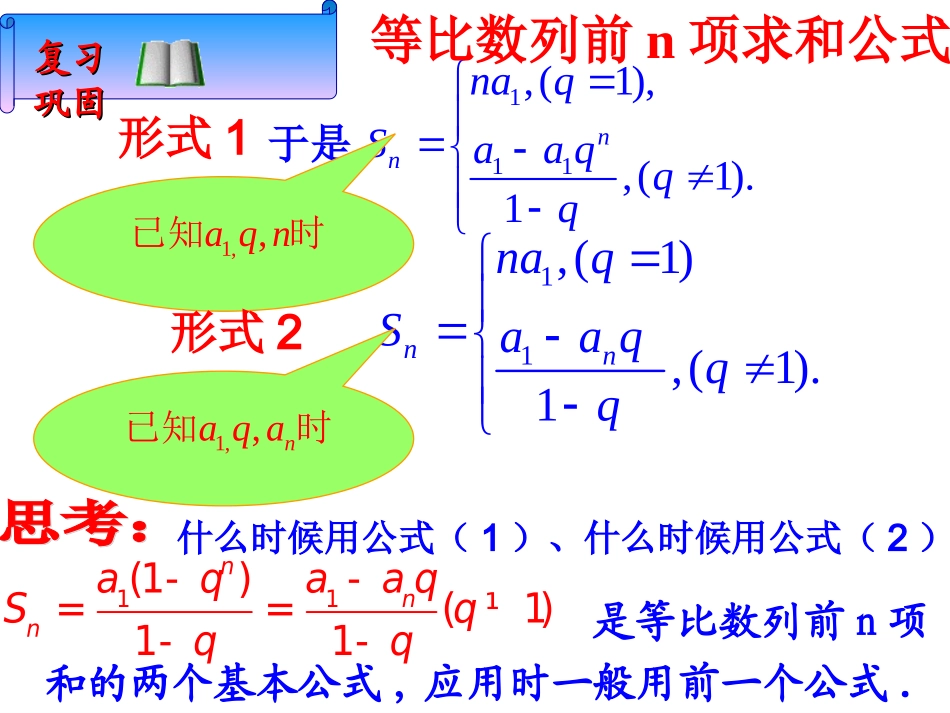
2025年1月28日成功是别人失败时自己还在坚持2012年大学世界排名第11名美国哥伦比亚大学2012年大学中国排名第11名华中科技大学111,(1),,(1).1nnnaqSaaqqq于是11,(1),(1).1nnnaqSaaqqq1,,aqn已知时1,,naqa已知时等比数列前n项求和公式形式1形式2什么时候用公式（1）、什么时候用公式（2）？复习复习巩固巩固11(1)(1)11nnnaqaaqSqqq--==¹--是等比数列前n项和的两个基本公式,应用时一般用前一个公式.数列{an}前n项和公式nnSAqA数列{an}是等比数列性质1.等比数列前n项和的函数特征性质2.Sk,S2k－Sk,S3k－S2k,…也是等比数列,1.已知数列{an}的前n项若数列{an}为等比数列，求实数a的值.132nnSa-=+学以致用性质4.性质3.22(1),nnnnnnnSSSSqqS23(1)nnnnSSqq21()nna,nnanS2.设等比数列的前项和为6936=3=SSSS若，则73学以致用1=nan等比数列的前2项的积30()1Ⅰn令12a21(1)14aqq2q2341(1)30.Saqqq解析解析260qq22240xx2(),ⅡnSx设2,2,14xx则成等比数列6x2,4,8,1642481630.nS解析解析302231()17Ⅲ（）nnnnnnnnSSqqqqSS2nq343nnnnSSqS3142230.解析解析30234231)2(1222)30或（nnnnnSSqqq4.设等比数列{an}的前n项和为Sn，已知S4＝1，S8＝17，求{an}的通项公式．解方法一在等比数列{an}中，由S4＝1，S8＝17，则q≠1，因此a1q4－1q－1＝1①a1q8－1q－1＝17②②÷①得q4＋1＝17，则q4＝16，∴q＝2，或q＝－2，由q＝2代入①得a1＝115，由q＝－2代入①得a1＝－15，所以数列{an}的通项公式为an＝115·2n－1或an＝－15·(－2)n－1.方法二q4＝S8－S4S4＝16，则q＝2，或q＝－2.又S4＝1，当q＝2时，由a1(1＋q＋q2＋q3)＝1得a1＝115，因此an＝a1qn－1＝2n－115；当q＝－2时，由a1(1＋q＋q2＋q3)＝1得a1＝－15.因此an＝a1qn－1＝－－2n－15.2025年1月28日让理想的雄鹰展翅高飞！再见祝同学们学习快乐、进步！祝同学们学习快乐、进步！