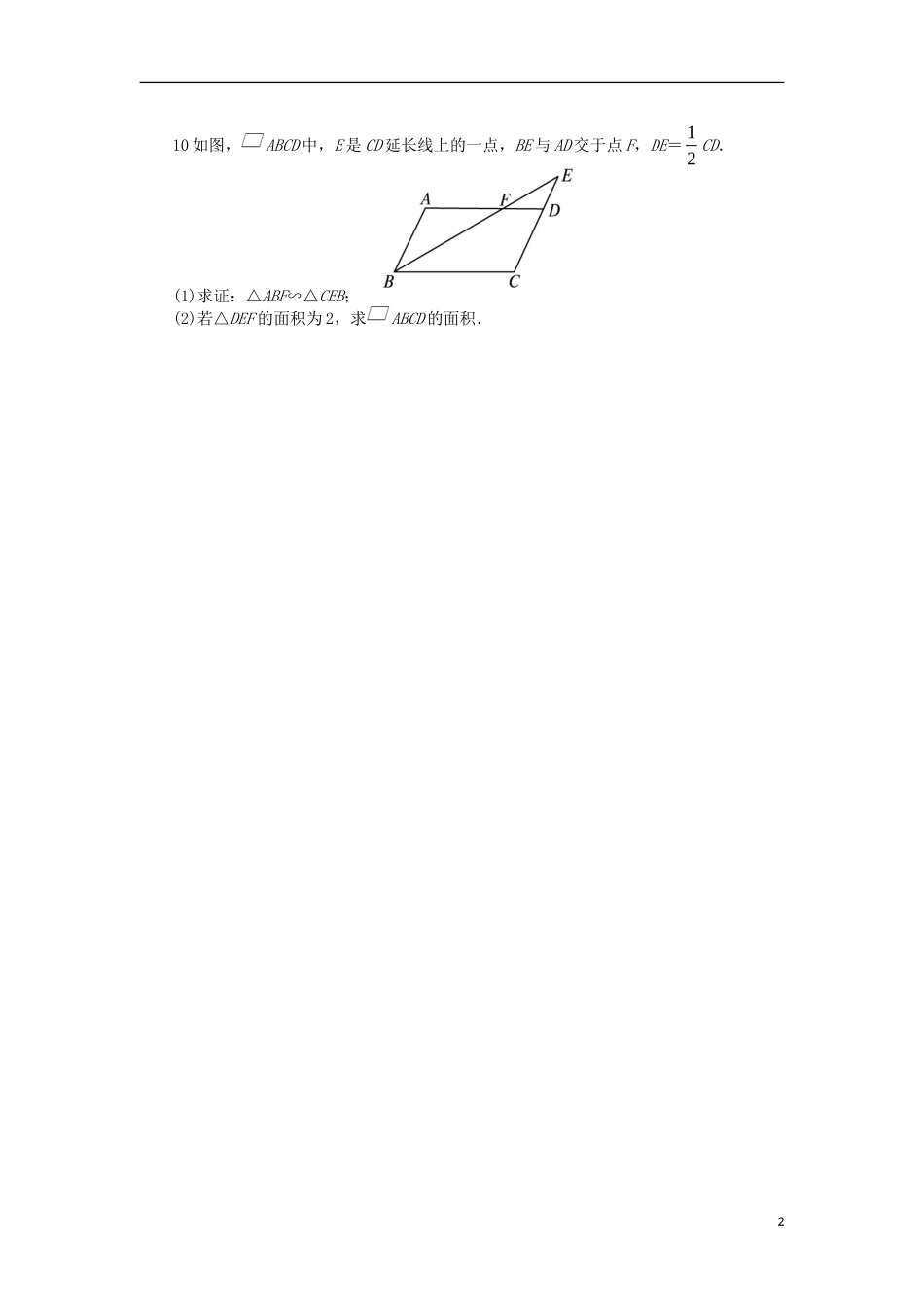
相似三角形的性质练习1三角形的一条中位线截该三角形所得的小三角形与原三角形的周长之比等于()A.14B.13C.12D.不确定2两个相似三角形对应中线分别长6cm和18cm,若较大三角形的面积是36cm2,则较小三角形的面积是()A.6cm2B.4cm2C.18cm2D.不确定3△ABC内切圆的半径r1=4,△A′B′C′内切圆的半径r2=6,且△ABC∽△A′B′C′,AB=2,则A′B′等于()A.3B.6C.9D.不确定4如图所示,D是△ABC中AB边上一点,过点D作DE∥BC交AC于点E.已知AD∶DB=1∶3,则△ADE与四边形BCED的面积比为()A.1∶3B.1∶9C.1∶15D.1∶165(情景题)有一块三角形铁片ABC,已知BC=12cm,高AD=8cm,要把它加工成一个矩形铁片,使矩形的一边在BC上,其余的两个顶点分别在AB,AC上,且矩形的长是宽的2倍.则加工成的铁片的面积为()A.18cm2或115249cm2B.20cm2或18cm2C.16cm2D.15cm26在比例尺为1∶500的地图上,测得一块三角形土地的周长为12cm,面积为6cm2,则这块土地的实际周长是__________m,实际面积是__________m2.7两个相似三角形对应中线之比是3∶7,周长之和为30cm,则它们的周长分别是______cm和______cm.8(探究题)在△ABC中,如图所示,BC=m,DE∥BC,DE分别交AB,AC于E,D两点,且S△ADE=S四边形BCDE,则DE=__________.9如图,在△ABC中,AB=14cm,59ADBD,DE∥BC,CD⊥AB,CD=12cm,求△ADE的面积.110如图,ABCD中,E是CD延长线上的一点,BE与AD交于点F,DE=12CD.(1)求证:△ABF∽△CEB;(2)若△DEF的面积为2,求ABCD的面积.2参考答案1答案:C小三角形与原三角形相似,其周长之比等于相似比.2答案:B相似比等于61183,则21139SS小大,故S小=19S大=19×36=4(cm2).3答案:A∵△ABC∽△A′B′C′,∴12rABrAB.∴426AB,∴A′B′=3.4答案:C因为DE∥BC,所以△ADE∽△ABC.又因为AD∶DB=1∶3,所以AD∶AB=1∶4,S△ADE∶S△ABC=1∶16,则所求的两部分面积比为1∶15.5答案:A本题有图(1)和图(2)两种情况,如图(1),矩形的长EF在BC上,G,H分别在AC,AB上,高AD交GH于K,设矩形的宽为xcm,则长为2xcm.由HG∥BC,得△AHG∽△ABC,得AK∶AD=HG∶BC(8-x)∶8=2x∶12247x(cm)S矩形EFGH=2x2=115249(cm2);如图(2),矩形的宽MN在BC上,类似地,可求得S矩形MNPQ=18(cm2).6答案:60150这块土地的实际形状与在地图上的形状是两个相似三角形,由比例尺可知,它们的相似比为1500,则实际周长是12×500=6000(cm)=60m;实际面积是6×5002=1500000(cm2)=150m2.7答案:921设两个三角形的周长分别为xcm,ycm,则x∶y=3∶7,x+y=30,解得x=9,y=21.8答案:22m∵DE∥BC,∴△ADE∽△ACB,又S△ADE+S四边形BCDE=S△ABC,S△ADE=S四边形BCDE,∴S△ADE=12S△ABC.∴212DEBC.∴212DEm.∴DE=22m.9答案:分析:先求出S△ABC,再由DE∥BC,可得△ABC∽△ADE,由2ADEABCSADSAB,可求3得S△ADE.解:∵CD⊥AB,∴S△ABC=12AB·CD=12×14×12=84(cm2).∵DE∥BC,∴△ABC∽△ADE,∴2ADEABCSADSAB.又59ADBD,∴514ADAB.∴258414ADES,∴S△ADE=757cm2.10答案:(1)证明:∵四边形ABCD是平行四边形,∴∠A=∠C,AB∥CD.∴∠ABF=∠E,∴△ABF∽△CEB.(2)解:∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD.∴△DEF∽△CEB,△DEF∽△ABF.∵DE=12CD,∴219DEFCEBSDESEC,214DEFABFSDESAB.∵S△DEF=2,∴S△CEB=18,S△ABF=8,∴S四边形BCDF=S△BCE-S△DEF=16,∴S四边形ABCD=S四边形BCDF+S△ABF=16+8=24.4