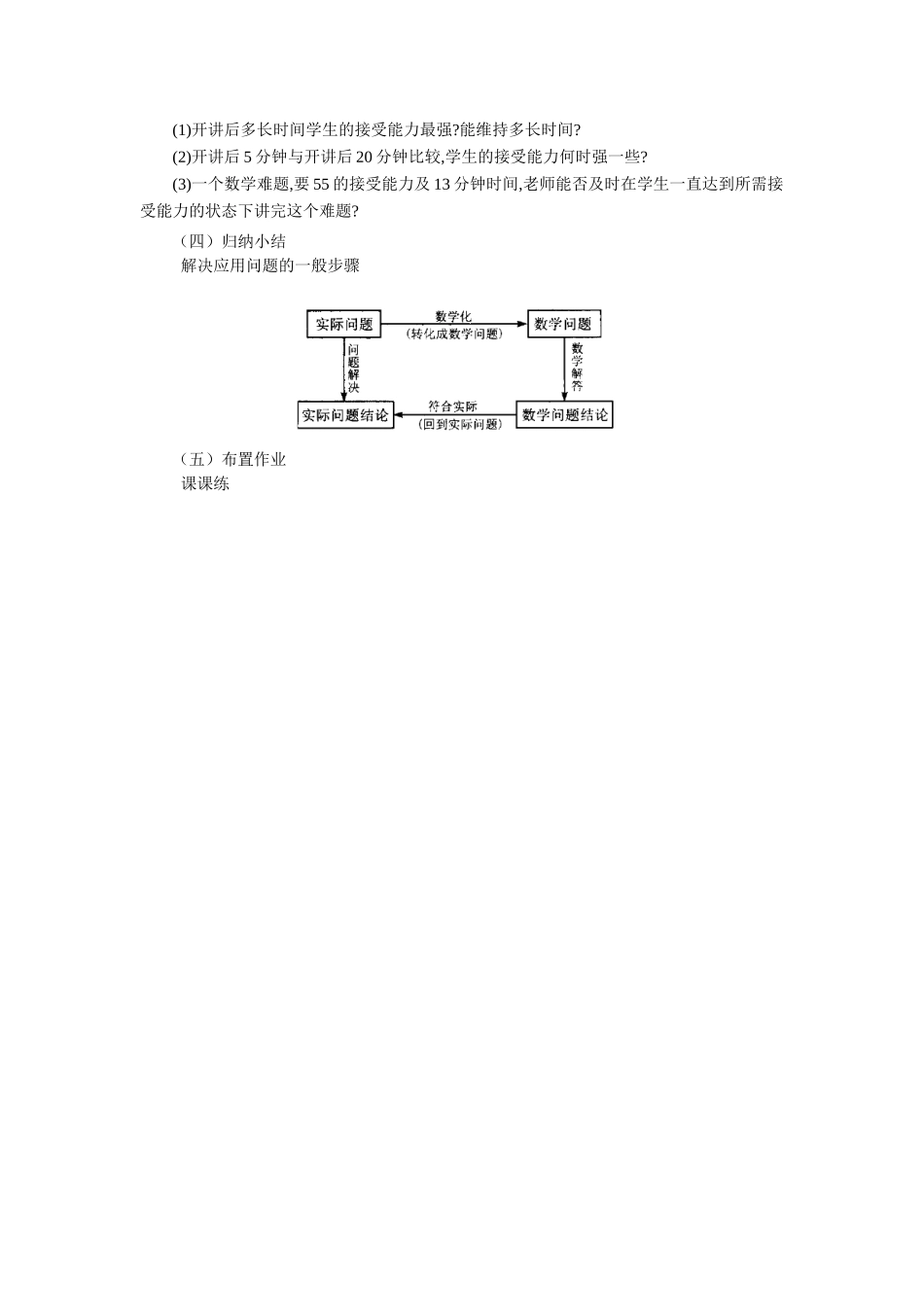
第33课函数模型及其应用(1)一、教学目标:1.知识与技能能够找出简单实际问题中的函数关系式,初步体会应用以学基本初等函数模型解决实际问题.2.过程与方法感受运用函数概念建立模型的过程和方法,体会函数模型在数学和其他学科中的作用。3.情感、态度、价值观体会运用函数思想处理现实生活和社会中的一些简单问题的实用价值.二、教学重点与难点:1.教学重点:运用函数模型解决一些实际问题.2.教学难点:将实际问题转变为数学模型.三、学法与教学用具1.学法:学生自主阅读教材,采用尝试、讨论方式进行探究.2.教学用具:多媒体四、教学设想:(一)创设情景1.我们已经学习了哪些基本初等函数?画出他们的图象,并指出各自的性质。2.解决应用问题的一般步骤有哪些?①审题:弄清题意,分清条件和结论,理顺数量关系;②建模:将文字语言转化为数学语言,利用数学知识,建立相应的数学模型;③解模:求解数学模型,得出数学结论;④还原:将用数学知识和方法得出的结论,还原为实际问题的意义.(二)实例探究1.一次函数模型例1.某厂在甲,乙两地的分厂各生产仪器12台和6台,现售给A地10台,B地8台.已知从甲调运1台至A,B两地的运费分别为400元和800元,从乙调运1台至A,B两地的运费分别为300元和500元.(1)要使总运费不超过9000元,共有几种方案?(2)求总运费最低时的调运方案与调运费.分析:设从甲地调入A地为台,列表如下:调出地甲地乙地调至地A地B地A地B地台数每台运费400800300500小计解答:设从甲地调入A地为台,总运费为,则=+++=,(1)由,得,所以即共有三种调运方案。(2)易见,当时,。答:略2.二次函数模型例2.在经济学中,函数的边际函数定义为某公司每月最多生产100台报警系统装置,生产台的收入函数为(单位:元),其成本函数(单位:元),利润是收入与成本之差。(1)求利润函数及边际利润函数;(2)利润函数与边际利润函数是否具有相同的最大值?阅读课本,并思考:边际利润函数的实际意义是什么?3.反比例函数模型例3.某地上年度电价为0.8元,年用电量为1亿度.本年度计划将电价调至0.55到0.75之间,经测算如电价调至元,则本年度新增用电量(亿度)与(-0.4)元成反比例.又当元时,.(收益=用电量(实际电量-成本价))(1)求与之间的函数关系式.(2)如每度电的成本价为0.3元,则电价调至多少时,本年度电力部门的收益将比上年度增加%?解答见《导学大课堂》4.幂指对函数模型见教材第61页例8、例9(三)巩固练习1.一家报刊推销员从报社买进报纸的价格是每份0.20元,卖出的价格是每份0.30元,卖不完的还可以以每份0.08元的价格退回报社.在一个月(以30天计算)有20天每天可卖出400份,其余10天只能卖250份,但每天从报社买进报纸的份数都相同,问应该从报社买多少份才能使每月所获得的利润最大?并计算每月最多能赚多少钱?2.学生的接受能力依赖于老师引入概念和描述问题所用的时间:开始时学生的兴趣激增,中间有一段不太长的时间学生的兴趣保持较理想的状态,随后学生的注意力开始分散.分析结果和实验表明,用表示学生的接受能力与时间有如下的关系:(1)开讲后多长时间学生的接受能力最强?能维持多长时间?(2)开讲后5分钟与开讲后20分钟比较,学生的接受能力何时强一些?(3)一个数学难题,要55的接受能力及13分钟时间,老师能否及时在学生一直达到所需接受能力的状态下讲完这个难题?(四)归纳小结解决应用问题的一般步骤(五)布置作业课课练