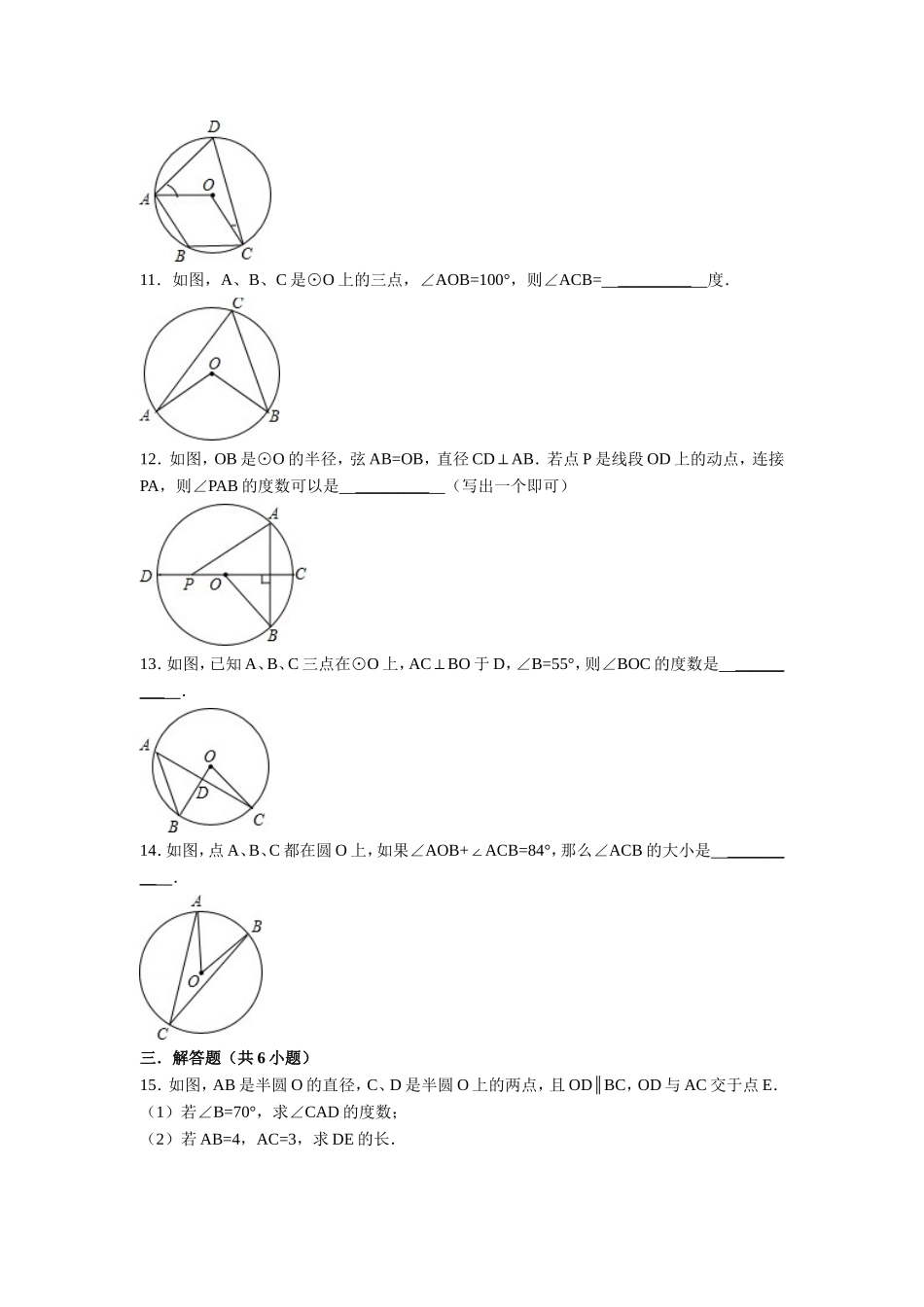
《2.1圆周角定理》同步练习6一.选择题(共8小题)1.如图,已知⊙O的直径CD垂直于弦AB,垂足为点E,∠ACD=22.5°,若CD=6cm,则AB的长为()A.4cmB.3cmC.2cmD.2cm2.如图,△ABC的顶点A、B、C均在⊙O上,若∠ABC+∠AOC=90°,则∠AOC的大小是()A.30°B.45°C.60°D.70°3.如图,在半径为1的⊙O中,∠AOB=45°,则sinC的值为()A.B.C.D.4.如图,在⊙O中,AB是直径,BC是弦,点P是上任意一点.若AB=5,BC=3,则AP的长不可能为()A.3B.4C.D.55.如图,已知A,B,C在⊙O上,为优弧,下列选项中与∠AOB相等的是()A.2∠CB.4∠BC.4∠AD.∠B+∠C6.如图,A、B、C、D四个点均在⊙O上,∠AOD=70°,AO∥DC,则∠B的度数为()A.40°B.45°C.50°D.55°7.如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠AOD等于()A.160°B.150°C.140°D.120°8.如图,⊙O的直径AB=2,弦AC=1,点D在⊙O上,则∠D的度数是()A.30°B.45°C.60°D.75°二.填空题(共6小题)9.如图,点A,B,C在⊙O上,若∠ABC=40°,则∠AOC的度数为_________.10.如图,点A、B、C、D在⊙O上,O点在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD=度.11.如图,A、B、C是⊙O上的三点,∠AOB=100°,则∠ACB=_________度.12.如图,OB是⊙O的半径,弦AB=OB,直径CD⊥AB.若点P是线段OD上的动点,连接PA,则∠PAB的度数可以是_________(写出一个即可)13.如图,已知A、B、C三点在⊙O上,AC⊥BO于D,∠B=55°,则∠BOC的度数是_________.14.如图,点A、B、C都在圆O上,如果∠AOB+∠ACB=84°,那么∠ACB的大小是_________.三.解答题(共6小题)15.如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.(1)若∠B=70°,求∠CAD的度数;(2)若AB=4,AC=3,求DE的长.16.已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D.(Ⅰ)如图①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;(Ⅱ)如图②,若∠CAB=60°,求BD的长.17.如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠BCD.(1)求证:CB∥PD;(2)若BC=3,sin∠BPD=,求⊙O的直径.18.如图,△ABC内接于半圆,AB是直径,过A作直线MN,∠MAC=∠ABC,D是弧AC的中点,连接BD交AC于G,过D作DE⊥AB于E,交AC于F.(1)求证:MN是半圆的切线;(2)求证:FD=FG.(3)若△DFG的面积为4.5,且DG=3,GC=4,试求△BCG的面积.19.如图,已知△ABC中,以AB为直径的半⊙O交AC于D,交BC于E,BE=CE,∠C=70°,求∠DOE的度数.20.如图,在半径为5cm的⊙O中,直径AB与弦CD相交于点P,∠CAB=50°,∠APD=80°.(1)求∠ABD的大小;(2)求弦BD的长.《2.1圆周角定理》同步练习6答案一.选择题(共8小题)1.B.2.C.3.B.4.A.5.A.6.D.7.C.8.C二.填空题(共6小题)9.80度10.60.11.5012.70°13.70°.14.28°三.解答题(共6小题)15.(1) AB是半圆O的直径,∴∠ACB=90°,又 OD∥BC,∴∠AEO=90°,即OE⊥AC,∠CAB=90°﹣∠B=90°﹣70°=20°,∠AOD=∠B=70°. OA=OD,∴∠DAO=∠ADO===55°∴∠CAD=∠DAO﹣∠CAB=55°﹣20°=35°;(2)在直角△ABC中,BC===. OE⊥AC,∴AE=EC,又 OA=OB,∴OE=BC=.又 OD=AB=2,∴DE=OD﹣OE=2﹣.16.解:(Ⅰ)如图①, BC是⊙O的直径,∴∠CAB=∠BDC=90°. 在直角△CAB中,BC=10,AB=6,∴由勾股定理得到:AC===8. AD平分∠CAB,∴=,∴CD=BD.在直角△BDC中,BC=10,CD2+BD2=BC2,∴易求BD=CD=5;(Ⅱ)如图②,连接OB,OD. AD平分∠CAB,且∠CAB=60°,∴∠DAB=∠CAB=30°,∴∠DOB=2∠DAB=60°.又 OB=OD,∴△OBD是等边三角形,∴BD=OB=OD. ⊙O的直径为10,则OB=5,∴BD=5.17.(1)证明: ∠D=∠1,∠1=∠BCD,∴∠D=∠BCD,∴CB∥PD;(2)解:连接AC, AB是⊙O的直径,∴∠ACB=90°, CD⊥AB,∴=,∴∠BPD=∠CAB,∴sin∠CAB=sin∠BPD=,即=, BC=3,∴AB=5,即⊙O的直径是5.18.解:(1)如右图所示, AB是直径,∴∠ACB=90°,∴∠CAB+∠ABC=90°, ∠MAC=∠ABC,∴∠CAB+∠MAC=90°...