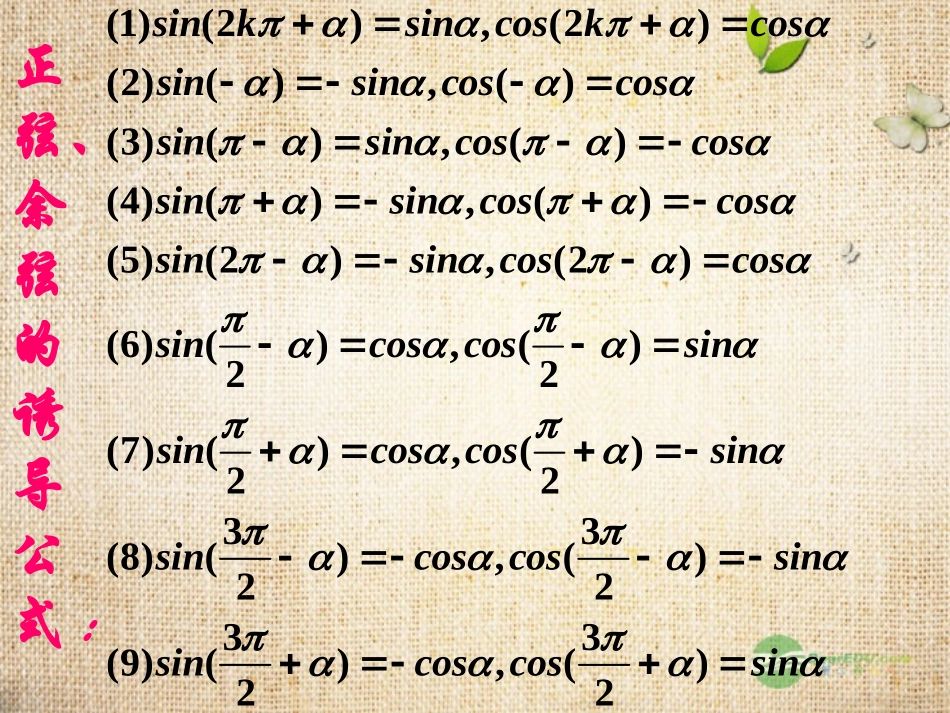广东省连州市高一数学《诱导公式》课件2VIP专享VIP免费

诱导公式诱导公式正弦、余弦的诱导公式:(1)(2),(2)(2)(),()(3)(),()(4)(),()(5)(2),(2)(6)(),()22(7)(2sinksincoskcossinsincoscossinsincoscossinsincoscossinsincoscossincoscossinsin),()233(8)(),()2233(9)(),()22coscossinsincoscossinsincoscossin诱导公式诱导公式()2kkZ奇变偶不变，符号看象限奇变偶不变，符号看象限..作用：诱导公式可以将任意角的三角函数转化为0-90角的三角函数值。.___30cos3sinsin4__________395tan)3(________;)855cos()2(_;__________600sin11000）（，则）（）已知（；）（：求下列各函数值：例fxxf练习.________)2cos()2sin(21.21.tan(-2010o)=_________.cos(80)ktan10021kk21kk21kk21kk4(10全国Ⅰ卷理2）记,那么A.B.-C.D.-B43.43.43.34.)(tan),23,2(,53)2cos(.3DCBA）的值。（，求）若（）的值；（，求）（）若（）（）化简（。）（）（）（）（）（）（为第三象限角，且：已知例f18603f512cos2;f1--cos--tan23-cos-2tan-sinf2练习练习..化简化简1.sin420°cos330°+sin(-690°)cos(-690°)=____.1.sin420°cos330°+sin(-690°)cos(-690°)=____.=sin60°cos30°+sin30°cos60°=sin60°cos30°+sin30°cos60°331112222333sin()cos()53222.sin()cos()sin(3)cos(4)22__________.11）的值。（），（），求（）（：已知例32sin65cos16cos3mm点评：观察已知角与所求角之间的关系，合理选用诱导公式，将不同名的化为同名，将不同角化为同角。.)3(sin)65sin(,41)6sin(.2.)4cos(,31)4sin(.12的值求已知的值求已知练习：xxx1sincoscossin842__________2coscos_____33sin______________6234tantantantan_______.5555ππαα,αααππθaθπθππππ；；；且则已知,则6.4.,5.作作业业123的值。求已知)2sin()cos(4)sin(3)cos(2,3)tan(.5的值。求已知)7cos(1,21)sin(.4