2.1数列的概念与简单表示法(共两课时)VIP免费

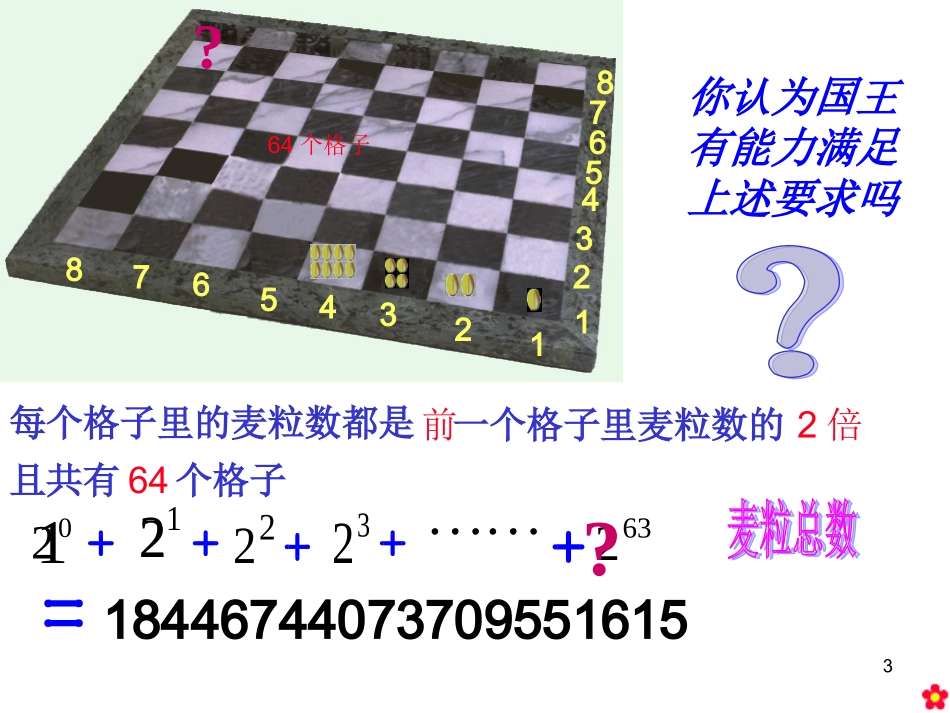
1“灵感不过是顽强的劳动而获得”的奖赏主备人：罗瑜唐强审核人：牟必继264个格子1223344551667788你想得到什么样的赏赐？陛下，赏小人一些麦粒就可以。OK请在第一个格子放1颗麦粒请在第二个格子放2颗麦粒请在第三个格子放4颗麦粒请在第四个格子放8颗麦粒依次类推……3456781567812334264个格子你认为国王有能力满足上述要求吗每个格子里的麦粒数都是前一个格子里麦粒数的2倍且共有64个格子2213263220212??184467440737095516154三角形数1,3,6,10,.…..正方形数1,4,9,16,……观察下列图形：提问：这些数有什么规律吗？5上述棋盘中各格子里的麦粒数按先后次序排成一列数：633222221，，，，，，，，4131211654321，，，，1，2，3，4……的倒数排列成的一列数：高一某班每次考试的名次由小到大排成的一列数：-1的1次幂，2次幂，3次幂，……排列成一列数：1111，，，，，，，1111无穷多个1排列成的一列数：三角形数：1，3，6，10，···正方形数：1，4，9，16，···6633222221，，，，654321，，，，1111，，，，，，，1111共同特点共同特点：1.都是一列数；2.都有一定的顺序12345，41，31，211，1，3，6，10，···1，4，9，16，···7定义：按一定顺序排列着的一列数称为问1：数列，2，改为13，…，65,2，，…，65331请问：是不是同一数列？问2:数列4改为：-1，1，-1，1……1，-1，1，-1……，请问：是不是同一数列？(数列具有有序性)想一想:数列与集合的区别是什么？（1）数列中是一列数，而集合中的元素不一定是数；（2）数列中的数是有一定顺序的，而集合中的元素没有顺序；（3）数列中的数可以重复，而集合中的元素不能重复。数列与集合概念的区别912345，，，，1111654321，，，，，，，，4131211633222221，，，，1111，，，数列中的每一个数叫做这个数列的项。各项依次叫做这个数列的第1项，第2项，······，第n项，······数列的分类(1)按项数分：项数有限的数列叫有穷数列项数无限的数列叫无穷数列(2)按项之间的大小关系分：递增数列，递减数列，摆动数列，常数列。有穷数列无穷数列有穷数列无穷数列无穷数列递增数列递增数列递减数列摆动数列常数列练习：P28观察10⑴全体自然数构成数列：⑵1996~2002年某市普通高中生人数（单位：万人）0，1，2，3,….82，93，105，119，129，130，132.构成数列⑶无穷多个3构成数列3，3，3，3，3,….⑷目前通用的人民币面额从大到小的顺序构成数列（单位:元）100，50，20，10，5，2，1，0.5，0.2，0.1，0.05，0.02，0.01.⑸-1的1次幂，2次幂，3次幂，4次幂构成数列-1，1，-1，1,….……递增数列递减数列常数列递增数列摆动数列以下数列属于哪种分类？1112345数列的一般形式可以写成：简记为,其中，，，，，naaaa321是数na1a第1项第2项第3项第n项的第n项与项数之间的关系可以用一个公式来表示，1111-12,,,,,22,12n632,,,,2131n1,,,,23n,,,,3511-n)1-(,,,,,11,,,1,1a2a3anana列的第1项或首项。02121112n)64,(*nNn}{n1{}n)35,(*nNn那么这个公式就叫做这个数列的通项公式。如果数列na12nnan1nannan)1(-=1na)(*Nn)(*Nn)(*Nnna是数列的第n项．12例1、写出下面数列的一个通项公式，使它的前4项分别是下列各数：.020264131211)5(;1,1,1,1)4(2516943;7,5,3,12;8,6,4,2)1(，，，）（；，，，；，，，）（）（136.1数列的概念解（1）数列的前4项与其项数的关系如下表：关系86424321项数nna由此得到，该数列的一个通项公式为例1、写出下面数列的一个通项公式，使它的前4项分别是下列各数：;8,6,4,2)1(222824261234nan2146.1数列的概念解（2）数列的前4项与其项数的关系如下表：由此得到，该数列的一个通项公式为例1、写出下面数列的一个通项公式，使它的前4项分别是下列各数：;7,5,3,1)2(关系75314321-1项数nna22112nan2-1233-1254-127例1、写出下面数列的一个通项公式，使它的前4项分别是下列各数：.020264131211)5(;1,...