正弦、余弦、正切函数的简单应用-(3)VIP免费

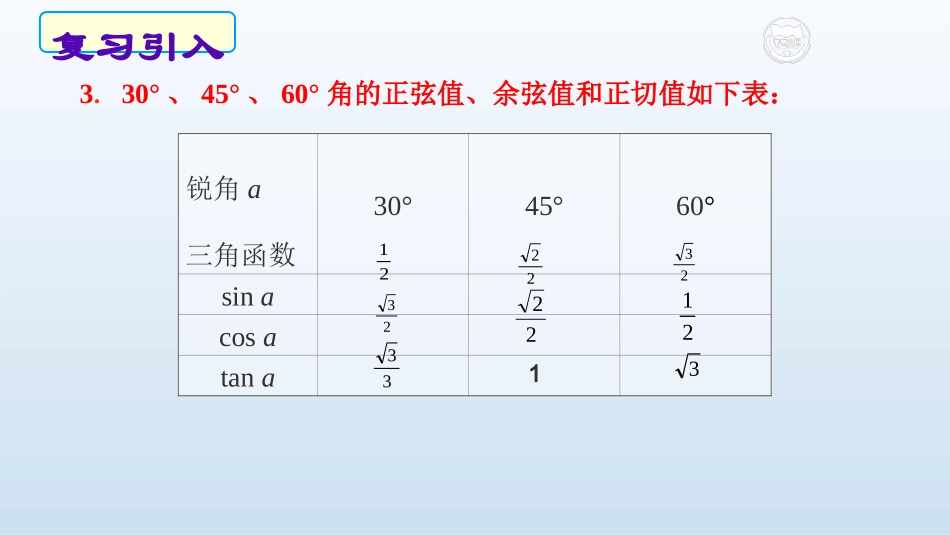
正弦、余弦、正切的简单应用汕头市潮阳区新宫学校陆永兰在直角三角形中,除直角外,由已知两元素求其余未知元素的过程叫解直角三角形.1.解直角三角形(1)三边之间的关系:a2＋b2＝c2（勾股定理）；2.解直角三角形的依据(2)两锐角之间的关系:∠A＋∠B＝90º；(3)边角之间的关系:tanA＝absinA＝accosA＝bc(必有一边)ＡＣＢabc别忽略我哦！复习引入3.30°、45°、60°角的正弦值、余弦值和正切值如下表：锐角a三角函数30°45°60°sinacosatana2122232322213313复习引入2.如图，已知Rt△ABC中，斜边BC上的高AD=3，cosB=，则AC的长为（）A．3B．3.75C．4.8D．545B1.如图，在Rt△ABC中，∠C=90°，∠B=30°，AB=8，则BC的长是（）43A.4B.4C.83D.43D落实基础1、当从低处观测高处的目标时,视线与水平线所成的锐角称为仰角.2、当从高处观测低处的目标时,视线与水平线所成的锐角称为俯角.铅直线水平线视线视线仰角俯角例题1:如图，航拍无人机从A处测得一栋建筑物顶部B的仰角为30°，测得底部C的俯角为60°，此时航拍无人机与建筑物的水平距离AD为90m，这栋建筑物有多高？【考点】解直角三角形的应用——仰角俯角问题【解析】(1)如图，∠BAD＝30°，∠DAC＝60°.(2)在Rt△ABD中，∠BAD＝30°，AD＝90m，所以可以利用解直角三角形的知识求出BD；(3)类似地，可以求出CD，进而求出BC的长度.解：如图，∠BAD＝30°，∠DAC＝60°，AD＝90∴BD=AD•tan30°=90×在Rt△ABD和Rt△ADC中，ADCDDACADBDBADtan,tanCD=AD•tan60°=90×33033答：这栋楼高为m3903∴BC=BD+CD=31203903303120变式变式11：：如图楼如图楼ABAB和楼和楼CDCD的水平距离为的水平距离为8080米，从楼顶米，从楼顶AA处处测得楼顶测得楼顶CC处的俯角为处的俯角为45°45°，测得楼底，测得楼底DD处的俯角为处的俯角为60°60°，，试求两楼高各为多少？试求两楼高各为多少？AABBCCDD45°AAEEDD（CC60°60°（8080米米EE1、建立基本模型2、构造直角三角形突破措施：（1）根据题目中的已知条件，将实际问题抽象为解直角三角形的数学问题，画出图形，弄清已知条件中各量之间的关系；（2）若三角形是直角三角形，根据边角关系进行计算；若三角形不是直角三角形，可通过添加辅助线构造直角三角形来解决．利用解直角三角形的知识解决实际问题的一般过程是：考点点拨如图,在平面上,过观察点O作一条水平线(向右为东)和一条铅垂线(向上为北),则从O点出发的视线与铅垂线所成的锐角,叫做观测的方位角(方向角）.30°45°45°北东西O南例如,图中“北偏东30°”是一个方位角;又如“西北”即指正西方向与正北方向所夹直角的平分线,此时的方位角为“北偏西45°”.例题2：如图，一艘海轮位于灯塔P的南偏东45°方向，距离灯塔30海里的A处，它沿正北方向航行一段时间后，到达位于灯塔P的北偏东30°方向上的B处，这时，海轮所在的B处距离灯塔P有多远？【解析】首先过点P作PCAB⊥于点C，根据Rt△APC中的45°，可求得CP的值；再利用解Rt△BPC求出即可.解：如图，过点P作PCAB⊥于点C在Rt△APC中，∠APC=45°,PA=30∴PC=PA•cos∠APC=30×在Rt△BPC中，∠B=30°PB=2PC=21522C2302152230答；海伦所在的B处距离灯塔有海里.变式变式22：：如图，一艘渔船由西往东航行，在点A测得海岛C位于北偏东60°的方向，前进20海里到达点B，此时，测得海岛C位于北偏东30°的方向，请问海岛C到航线AB的距离CD为多少海里？【解析】(1)根据方位角的定义及余角的性质,可求∠CAD和∠CBD；(2)再由三角形外角的性质得到∠CAD=∠ACB=30°，从而得到AB=BC=20；(3)解Rt△BDC，求出CD即可.点评：求三角形的边或高的问题，一般可以转化为解直角三角形的问题，解决的方法就是作高线！注意以下要点：（1）将实际问题抽象为数学问题（画出平面图形，构造出直角三角形转化为解直角三角形的问题）；（2）根据题目已知条件选用适当锐角三角函数或边角关系去解直角三角形，得到数学问题的答案，再转化得到实际问题的答案．本考点的题型一般为解答题，难度适中.解答本考点的有关题目，关键在于借助实际问题中的俯角、仰角、方位角等构造直角三角形并解直角三角形.课堂小结练习1.如图...