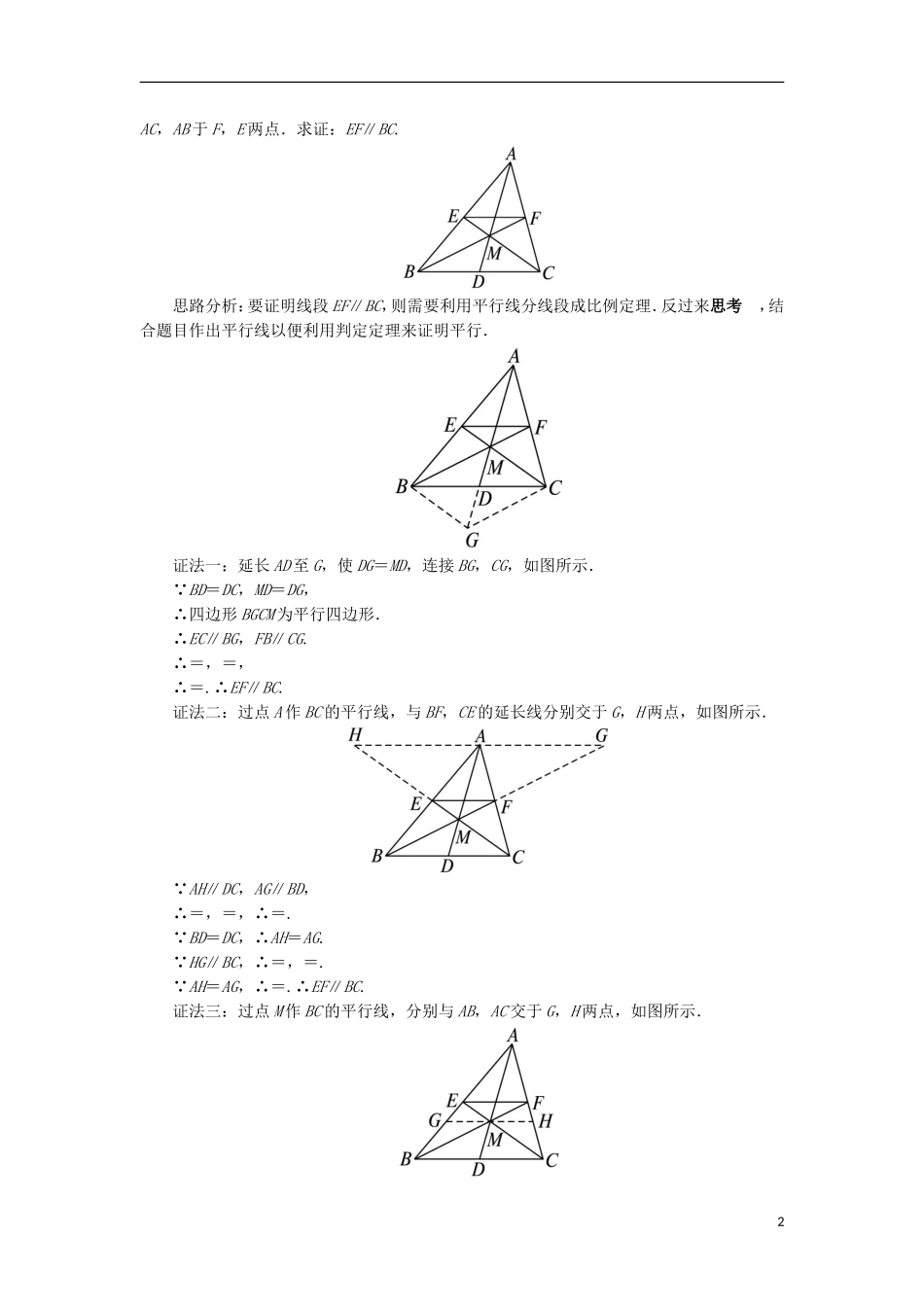
三相似三角形的判定及性质课堂探究探究一判定三角形相似判定两个三角形相似时,关键是分析已知哪些边对应成比例,哪些角对应相等,根据三角形相似的判定定理,寻找推导出结论的条件.【典型例题1】如图,已知==,求证:△ABD∽△ACE.思路分析:证明三角形相似,关键在于找到符合定理的条件.由题目所给条件,应需再找出角的相等关系.证明:因为==,所以△ABC∽△ADE.所以∠BAC=∠EAD,∠BAC-∠DAC=∠EAD-∠DAC,即∠DAB=∠EAC.又=,即=,所以△ABD∽△ACE.点评本题中,∠DAB与∠EAC的相等关系,不易直接找到,这里用∠BAC=∠EAD,在∠BAC和∠EAD中分别减去同一个角∠DAC,间接证明.探究二判定直角三角形相似直角三角形相似的判定方法很多,既可根据一般三角形相似的判定方法判定,又有其独特的判定方法,在求证、识别的过程中,可由已知条件结合图形特征,确定合适的方法.【典型例题2】如图,已知在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点,求证:△ADQ∽△QCP.思路分析:由于这两个三角形都是直角三角形,且已知条件是线段间的关系,故考虑证明对应边成比例,即只需证明=即可.证明:在正方形ABCD中,∵Q是CD的中点,∴=2.∵=3,∴=4.又BC=2DQ,∴=2.在△ADQ和△QCP中,==2,∠C=∠D=90°,∴△ADQ∽△QCP.规律总结证明直角三角形相似的方法主要有除直角外的一组锐角对应相等或两边对应成比例.本题就是利用了=两直角边对应成比例证明.探究三证明两直线平行常利用引理来证明两直线平行,其关键是证明其对应线段成比例,这样就转化为证明线段成比例,其证明方法有:利用中间量,转化成线段成比例,两者结合使用证明.【典型例题3】如图,在△ABC中,D是BC的中点,M是AD上一点,BM,CM的延长线分别交1AC,AB于F,E两点.求证:EF∥BC.思路分析:要证明线段EF∥BC,则需要利用平行线分线段成比例定理.反过来思考,结合题目作出平行线以便利用判定定理来证明平行.证法一:延长AD至G,使DG=MD,连接BG,CG,如图所示.∵BD=DC,MD=DG,∴四边形BGCM为平行四边形.∴EC∥BG,FB∥CG.∴=,=,∴=.∴EF∥BC.证法二:过点A作BC的平行线,与BF,CE的延长线分别交于G,H两点,如图所示.∵AH∥DC,AG∥BD,∴=,=,∴=.∵BD=DC,∴AH=AG.∵HG∥BC,∴=,=.∵AH=AG,∴=.∴EF∥BC.证法三:过点M作BC的平行线,分别与AB,AC交于G,H两点,如图所示.2则=,=,∴=.∵BD=DC,∴GM=MH.∵GH∥BC,∴=,=.∵GM=MH,∴=.∴EF∥BC.规律总结要证明EF∥BC,想通过角之间的关系达到目的显然是不可能的,而要利用成比例线段判定两条直线平行的判定定理,图中又没有平行条件,因此要设法作出平行线,以便利用判定定理.在作平行线时,要充分考虑到中点D的应用.探究四易错辨析易错点:因对应元素不确定而引起错误【典型例题4】在△ABC中,AB>BC>AC,D是AC的中点,过D作直线l,使截得的三角形与原三角形相似,这样的直线有________条.错解:如图,过点D作DE1∥BC,此时∠AE1D=∠B,∠A=∠A,所以△ABC∽△AE1D;过点D作DE2∥AB,此时∠CE2D=∠B,∠C=∠C,所以△ABC∽△DE2C.答案:2错因分析:本题为探索性题目,由于对应元素不确定,因而存在多种情况,只考虑两种情况不够全面.正解:如图,过点D作DE1∥BC,此时∠AE1D=∠B,所以△ABC∽△AE1D;在线段AB上取一点E2,使∠ADE2=∠B,此时△ADE2∽△ABC.同理过点D作DE3∥AB,使∠DE3C=∠B;在线段BC上取一点E4,使∠E4DC=∠B,都能使截得的三角形与原三角形相似,因此共有4条直线符合要求.答案:43