一元一次不等式组和它的解法VIP免费

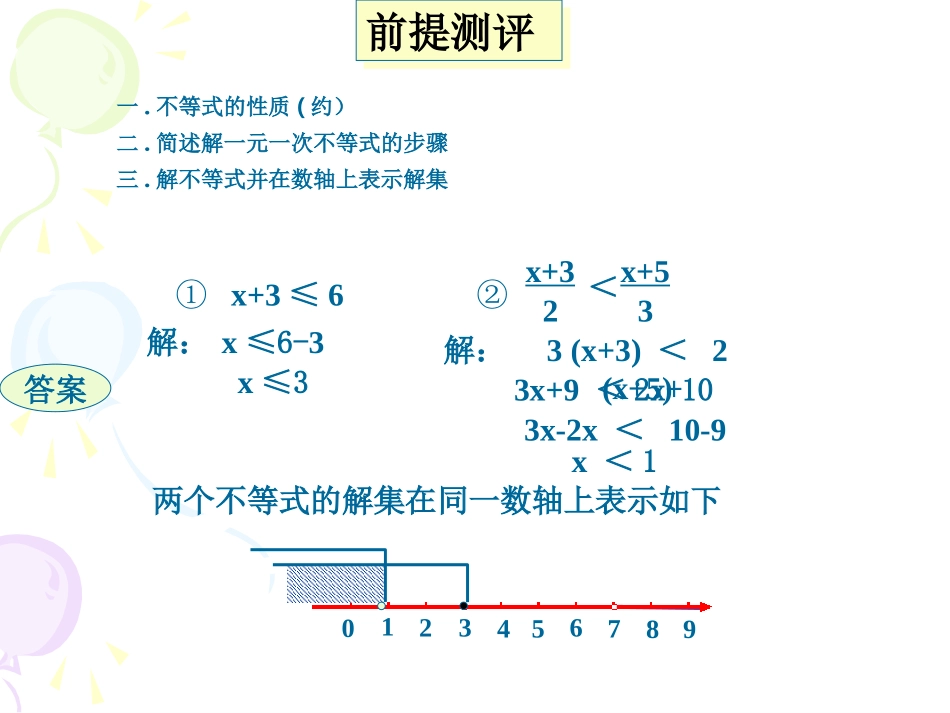
一.不等式的基本性质有哪些。二.简述解一元一次不等式的步骤。三.解不等式并在同一数轴上表示解集前提测评前提测评①x+3≤6②答案x+32＜x+53一.不等式的性质(约）二.简述解一元一次不等式的步骤三.解不等式并在数轴上表示解集①x+3≤6②答案x≤6-33(x+3)＜2(x+5)3x+9＜2x+10x≤33x-2x＜10-9解：解：两个不等式的解集在同一数轴上表示如下前提测评前提测评x＜1x+32x+53＜0765421389一元一次不等式组和它的解法设物体A的质量为x克，每个砝码的质量为1克从图中可以看出物体A的质量大于2g并且小于3g,即x>2与x<3都成立.一元一次不等式x>2与x<3合在一起,就组成了一个一元一次不等式组一元一次不等式组,记作.3,2xx从数轴上看前面两个不等式组解集的情况不等式组的解集（请观察不等式的解集在数轴上的反映：射线与线段）结论几个不等式解集的公共部分叫做由它们所组成不等式组的解集。x＞2x＜3x+3≤6x+52＜x+33(x≤3)(x＜1)0765421389x£¾43x-2x£¾3+1½â²»µÈʽ¢Ù3x-1£¾2x+3x£¾-2x-2x＜1+1解不等式②x-1＜2x+13x-1£¾2x+3¢Ùx-1＜2x+1②例一解不等式组3x-1＞2x-3x-1＜2x-1②①解不等式组解不等式组（求不等式组解集的过程）分析所以原不等式的解集ｘ＞４二.解不等式组2(x+2)＜x+53(x-2)+8＞2x①②解答二.解不等式组2(x+2)＜x+53(x-2)+8＞2x①②解：解不等式①，得解不等式②，得x＜1x＞-2在数轴上表示不等式①，②的解集所以，原不等式的解集是-2＜x＜1例1.求下列不等式组的解集:.7,3)1(xx.5,2)3(xx.4,0)4(xx7x解:原不等式组的解集为2x解:原不等式组的解集为2x解:原不等式组的解集为0x解:原不等式组的解集为同大取大-5-20-3-1-40765421389-3-2-104213.3,2)2(xx-5-20-3-121-4例1.求下列不等式组的解集:.7,3)5(xx.5,2)6(xx.4,1)7(xx.4,0)8(xx3x解:原不等式组的解集为5x解:原不等式组的解集为1x解:原不等式组的解集为4x解:原不等式组的解集为同小取小0765421389-5-2-3-1-40-7-6-3-2-1042135-5-20-3-11-4-6例1.求下列不等式组的解集:.7,3)9(xx.5,2)10(xx0765421389-3-2-104213573x解:原不等式组的解集为25x解:原不等式组的解集为41x解:原不等式组的解集为04x解:原不等式组的解集为大小小大中间找-5-20-3-11-4-6-5-2-3-1-40-7-6.4,1)11(xx.4,0)12(xx例1.求下列不等式组的解集:.7,3)13(xx.5,2)14(xx.4,1)15(xx0765421389解:原不等式组无解.解:原不等式组无解.解:原不等式组无解.解:原不等式组无解.大大小小解不了-5-2-3-1-40-7-6-3-2-1042135-5-20-3-11-4-6.4,0)16(xx比一比：看谁反应快运用规律求下列不等式组的解集：.3,2)1(xx.5,2)2(xx.7,3)3(xx.4,0)4(xx.7,3)5(xx.4,1)6(xx.7,3)7(xx.4,0)8(xx21)9(xx0201)10(xx0201)11(xx4263)12(xx1.同大取大，2.同小取小；3.大小小大中间找，4.大大小小解不了。1.1.使不等式使不等式x+7≥0x+7≥0与与2x-1<02x-1<0都成立的都成立的xx的的取值范围是取值范围是。。2.2.把把-102x-1<3｛达标测评达标测评5．若不等式组无解，求m的取值范围。0mx01x一选择题1.选择下列不等式组的解集①x≥-1x≥2x≥2x≥-1-1≤x≤2无解②x＜-1x＜2x＜2x＜-1-1＜x＜2无解无解无解③x≥-1x≥-1x＜2x＜2-1≤x＜2x＜-1x＜-1④x≥2x≥2-1＜x≥2上页下页ACBBBCDDDCAABDCA2.不等式组达标测评达标测评x+2＞0x-1≥0的解集在数轴上表示正确的是3.下列不等式中，解集为x＜-4的是x+＞0x+4＞0x-5＜0x-5＜0x-5＞0x+4＜0上页下页ABCCDAB学习小结学习小结一.解一元一次不等式组的两个解题步骤1.求出不等式组中各个不等式的解集；2.利用数轴，求出这些不等式解集的公共部分，也就是求出了这个不等式组的解集。二.一元一次不等式组的解集图析不等式组的解集不等式组的解集bxaxbxaxbxaxbxax不等式组ababababbxax无解数轴表示解集ba