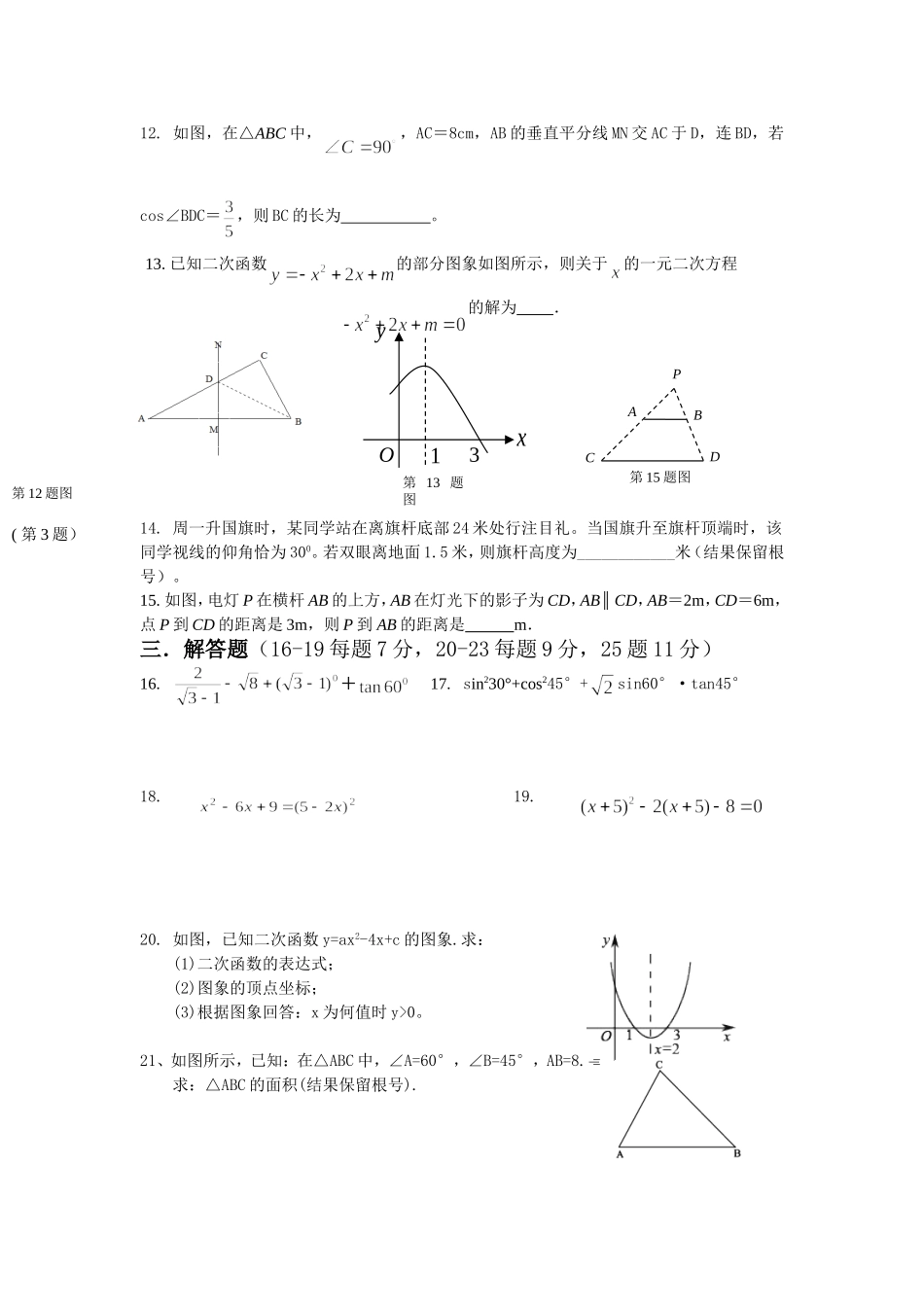
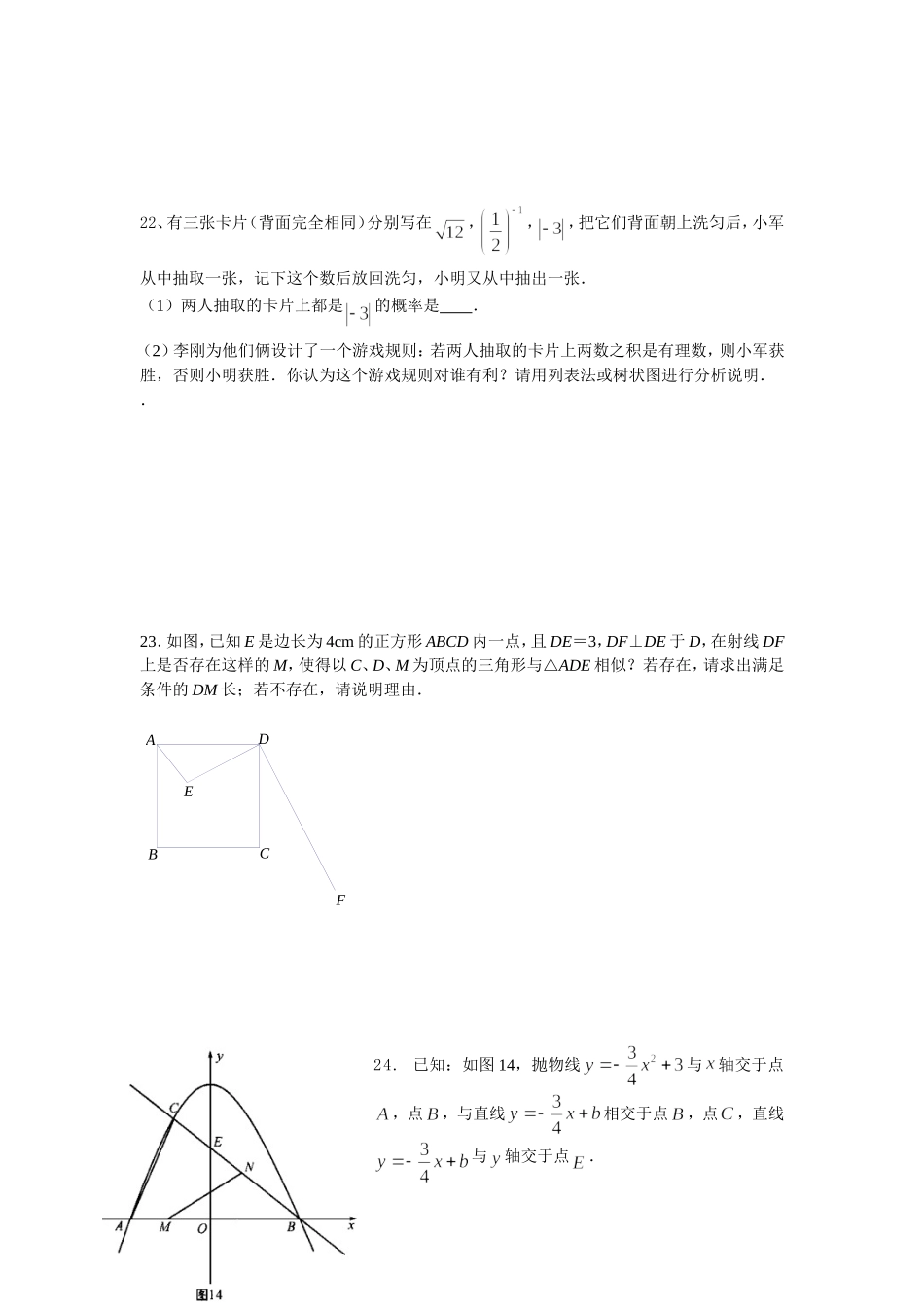
段考数学试卷一.选择题(每题3分,共18分)1.已知a=,b=,则a+b-ab的值是()A.3B.4C.5D.22.在△ABC中,已知+(cotB-1)2=0,则∠C为()A.30°B.135°C.105°D.120°3.已知函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c+2=0的根的情况是()A.无实数根B.有两个相等的实数根C.有两个异号的实数根D.有两个同号不等的实数根4.在同一坐标系中一次函数和二次函数的图象可能为()5.关于x的一元二次方程mx2-3x-4=4x+3有实数根,则m的取值范围是().A.m>-B.m≤-且m≠0C.m≥-D.m≥-且m≠06.如图,AB是斜靠在墙上的梯子,梯脚距墙2米,梯子上的D点距墙1.8米,BD长0.6米,则梯子的长为()A、5.60米B、6.00米C、6.10米D、6.20米二.填空题(每题3分,共27分)7.将抛物线向左平移一个单位,再向下平移两个单位后,得到的抛物线解析式是8.抛物线与轴只有一个公共点,则的值为.9.如图为二次函数y=ax2+bx+c的图象,在下列说法中:①ac<0;②方程ax2+bx+c=0的根是x1=-1,x2=3③a+b+c>0④当x>1时,y随x的增大而增大。正确的说法有_____________。(把正确答案的序号填在横线上)10.若抛物线y=x2-(m-3)x+2的对称轴为y轴,则m=_________.11.抛物线y=ax2+bx+c经过点A(0,-3),B(2,-3),C(-2,5),则该抛物线上纵坐标为5的另一个点D的坐标是___________。第3题图xyO–3OxyOxyOxyOxyABCDDBA第6题图第9题图12.如图,在△ABC中,,AC=8cm,AB的垂直平分线MN交AC于D,连BD,若cos∠BDC=,则BC的长为。13.已知二次函数的部分图象如图所示,则关于的一元二次方程的解为.14.周一升国旗时,某同学站在离旗杆底部24米处行注目礼。当国旗升至旗杆顶端时,该同学视线的仰角恰为300。若双眼离地面1.5米,则旗杆高度为____________米(结果保留根号)。15.如图,电灯P在横杆AB的上方,AB在灯光下的影子为CD,AB∥CD,AB=2m,CD=6m,点P到CD的距离是3m,则P到AB的距离是m.三.解答题(16-19每题7分,20-23每题9分,25题11分)16.+17.sin230°+cos245°+sin60°·tan45°18.19.20.如图,已知二次函数y=ax2-4x+c的图象.求:(1)二次函数的表达式;(2)图象的顶点坐标;(3)根据图象回答:x为何值时y>0。21、如图所示,已知:在△ABC中,∠A=60°,∠B=45°,AB=8.求:△ABC的面积(结果保留根号).(第3题)第15题图ABCDPyxO13第13题图第12题图FECDBA22、有三张卡片(背面完全相同)分别写在,,,把它们背面朝上洗匀后,小军从中抽取一张,记下这个数后放回洗匀,小明又从中抽出一张.(1)两人抽取的卡片上都是的概率是.(2)李刚为他们俩设计了一个游戏规则:若两人抽取的卡片上两数之积是有理数,则小军获胜,否则小明获胜.你认为这个游戏规则对谁有利?请用列表法或树状图进行分析说明..23.如图,已知E是边长为4cm的正方形ABCD内一点,且DE=3,DF⊥DE于D,在射线DF上是否存在这样的M,使得以C、D、M为顶点的三角形与△ADE相似?若存在,请求出满足条件的DM长;若不存在,请说明理由.24.已知:如图14,抛物线与轴交于点,点,与直线相交于点,点,直线与轴交于点.(1)写出直线的解析式.(2)求的面积.(3)若点在线段上以每秒1个单位长度的速度从向运动(不与重合),同时,点在射线上以每秒2个单位长度的速度从向运动.设运动时间为秒,请写出的面积与的函数关系式,并求出点运动多少时间时,的面积最大,最大面积是多少?