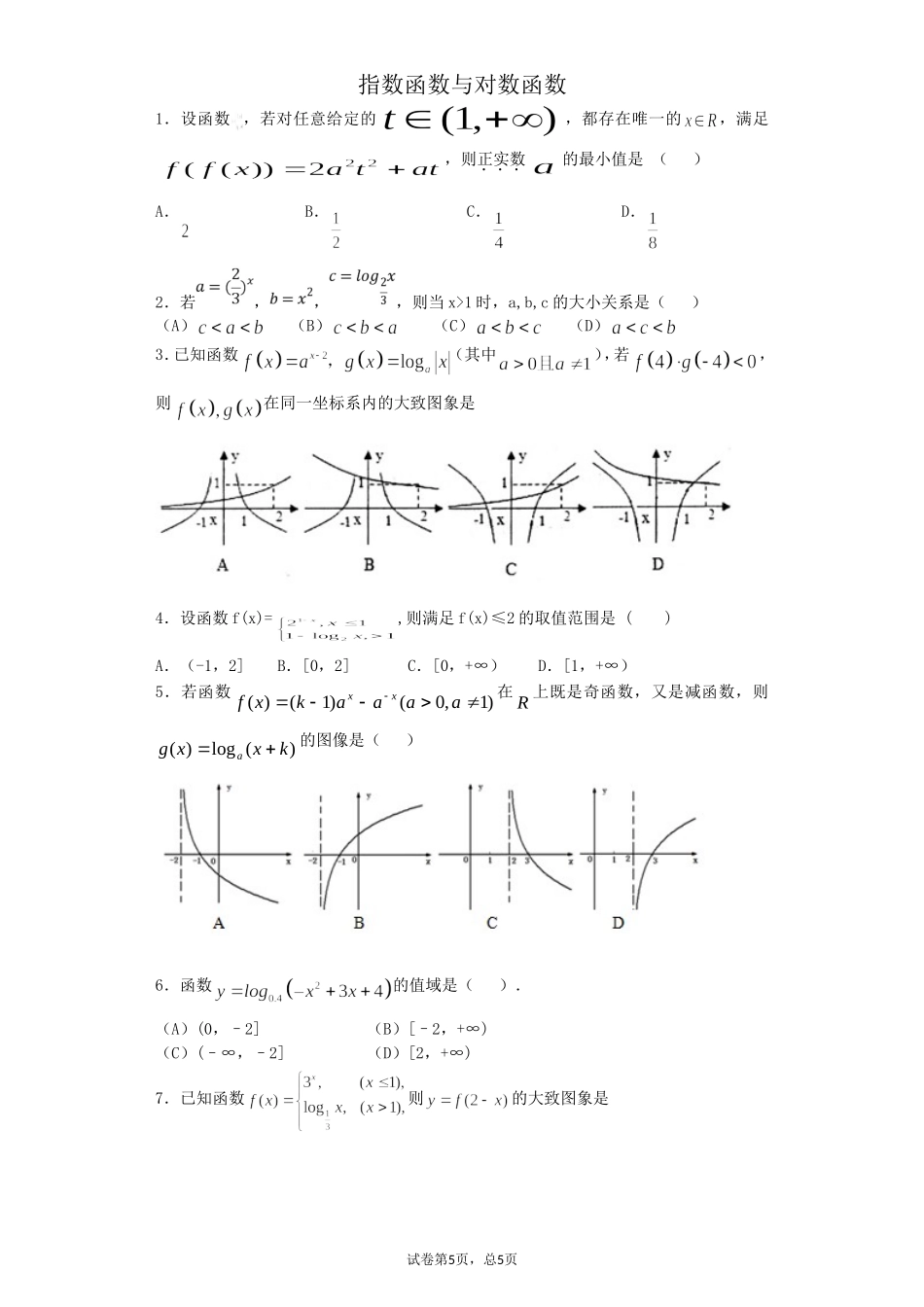
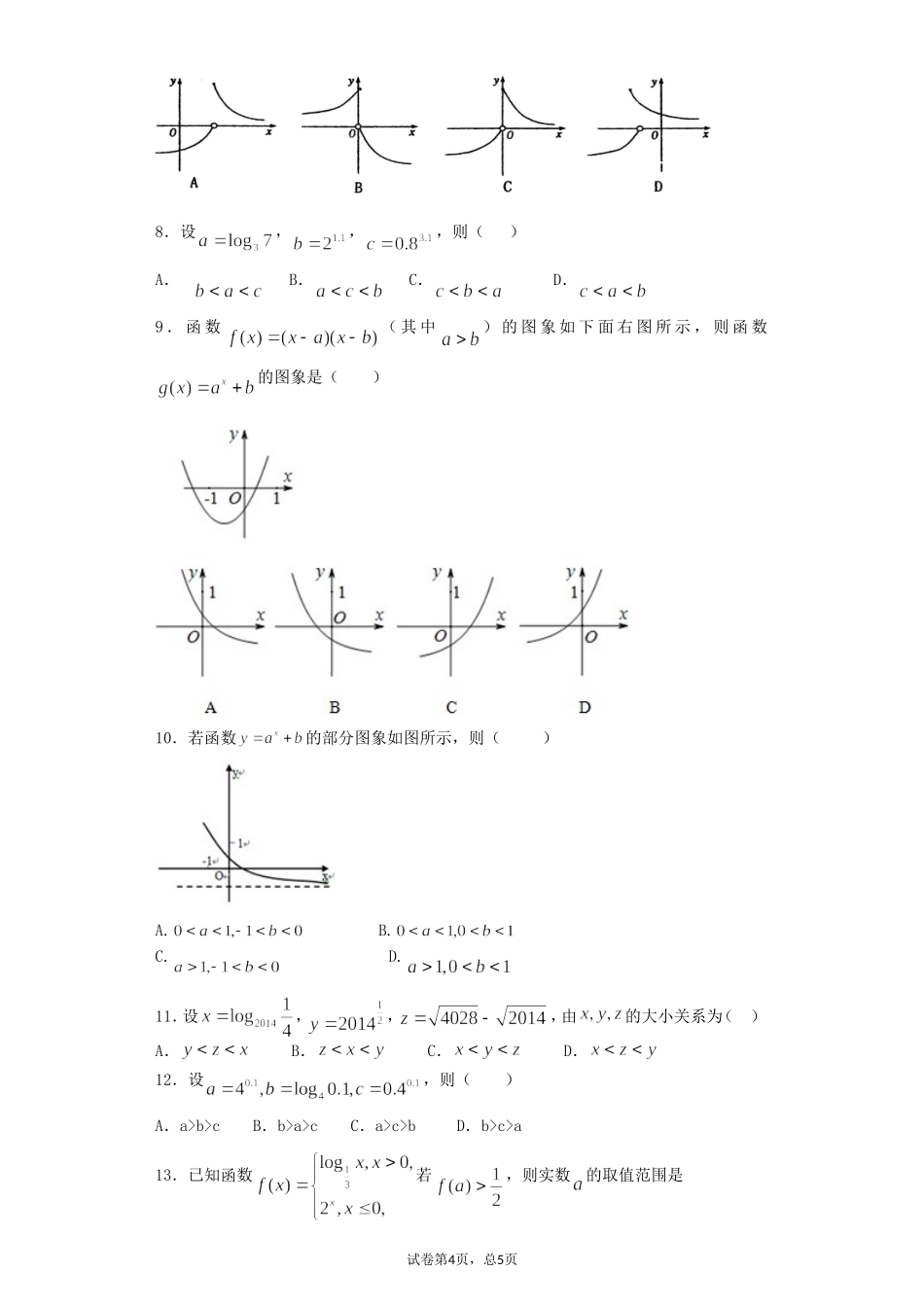
指数函数与对数函数1.设函数,若对任意给定的,都存在唯一的,满足,则正实数的最小值是()A.B.C.D.2.若,,,则当x>1时,a,b,c的大小关系是()(A)(B)(C)(D)3.已知函数(其中),若,则在同一坐标系内的大致图象是4.设函数f(x)=,则满足f(x)≤2的取值范围是()A.(-1,2]B.[0,2]C.[0,+∞)D.[1,+∞)5.若函数)1,0()1()(aaaakxfxx在R上既是奇函数,又是减函数,则)(log)(kxxga的图像是()6.函数的值域是().(A)(0,–2](B)[–2,+∞)(C)(–∞,–2](D)[2,+∞)7.已知函数则的大致图象是试卷第5页,总5页8.设,,,则()A.B.C.D.9.函数(其中)的图象如下面右图所示,则函数的图象是()10.若函数的部分图象如图所示,则()A.B.C.D.11.设,,,由的大小关系为()A.B.C.D.12.设,则()A.a>b>cB.b>a>cC.a>c>bD.b>c>a13.已知函数若,则实数的取值范围是试卷第4页,总5页(A)(B)(C)(D)14.已知函数,则.15.函数在区间(-∞,1)内递增,则a的取值范围是。16.当时,函数的图像恒过点A,若点A在直线上,则的最小值为_________.17.已知函数满足:x4,则=;当x<4时=,则=.18.已知函数,且的图象恒过点,若角的终边经过点,则的值等于_______.19.不等式的解集为.20.。21.若实数满足,则的最小值为________.22.(本小题满分12分)计算:(1)(2)23.(本题满分10分)(1)已知,计算式子的值;(2)设25abm,且11ab=2,求的值。试卷第5页,总5页24.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分已知函数()(0,1,)xbfxaaabR.(1)若()fx为偶函数,求b的值;(2)若()fx在区间2,上是增函数,试求a、b应满足的条件.25.(13分)已知函数,(1)判断函数的奇偶性;(2)若对任意的,都有不等式恒成立,求实数的取值范围。26.(本题满分12分)已知函数,函数.(1)求函数与的解析式,并求出,的定义域;(2)设,试求函数的最值.27.(本小题满分12分)已知函数,定义域为,求函数的最值,并指出取得最值时相应自变量的取值.28.已知函数.试卷第4页,总5页(1)当时,求函数的定义域;(2)若关于的不等式的解集是,求的取值范围.29.已知函数()lg(2)lg(2)fxxx.(Ⅰ)求函数()yfx的定义域;(Ⅱ)判断函数()yfx的奇偶性;(Ⅲ)若(2)()fmfm,求的取值范围.30.已知函数.(1)若函数为奇函数,求实数的值;(2)若对任意的,都有成立,求实数的取值范围.试卷第5页,总5页参考答案1.B试题分析:当时,,值域为(0,1],所以;当时,,值域为,所以;当时,,值域为,则,故,当时,值域为,当时,值域为,因为,所以,对称轴为,故在上是增函数,则在上的值域为,即),有题意知,,解得,故正实数a的最小值为;考点:指数函数的解析式以及定义2.A试题分析:在同一坐标内作出三个函数的图象,然后根据条件,在x>1右侧任作一条直线,则看三个交点的纵坐标,即三个函数相应函数值.在同一坐标内作出三个函数的图象,如图所示:c<a<b,故答案为A考点:函数值大小比较3.B.试题分析: ,又f(4)g(-4)<0,∴g(-4)=,∴0<a<1,∴f(x)在R上单调递减,过点(2,1),g(x)为偶函数,其图象在(0,+∞)上均单调递减,故选B.考点:考查了函数的图象.点评:解本题的关键是掌握对数函数和指数函数的性质和图象.4.C试题分析:或或或或.故C正确.答案第9页,总9页考点:1分段函数;2指数函数,对数函数不等式.5.A试题分析:由题可知,函数)1,0()1()(aaaakxfxx在R上既是奇函数,即满足,解得,又函数是减函数,则的范围为,因此对于)(log)(kxxga,底数的范围为,为减函数,向左移动两个单位,即为图像A;考点:函数的奇偶性与单调性6.B试题分析:为使有意义,须,解得,此时,,又对数的底数小于,所以,故选.考点:1.函数的定义域、值域;2.对数函数、二次函数的性质.7.A试题分析:对应函数,当时,,因此与轴得到交点在轴负半轴,观察图象,故答案为A.考点:函数图象的判断.8.D试题分析:因为,,,所...