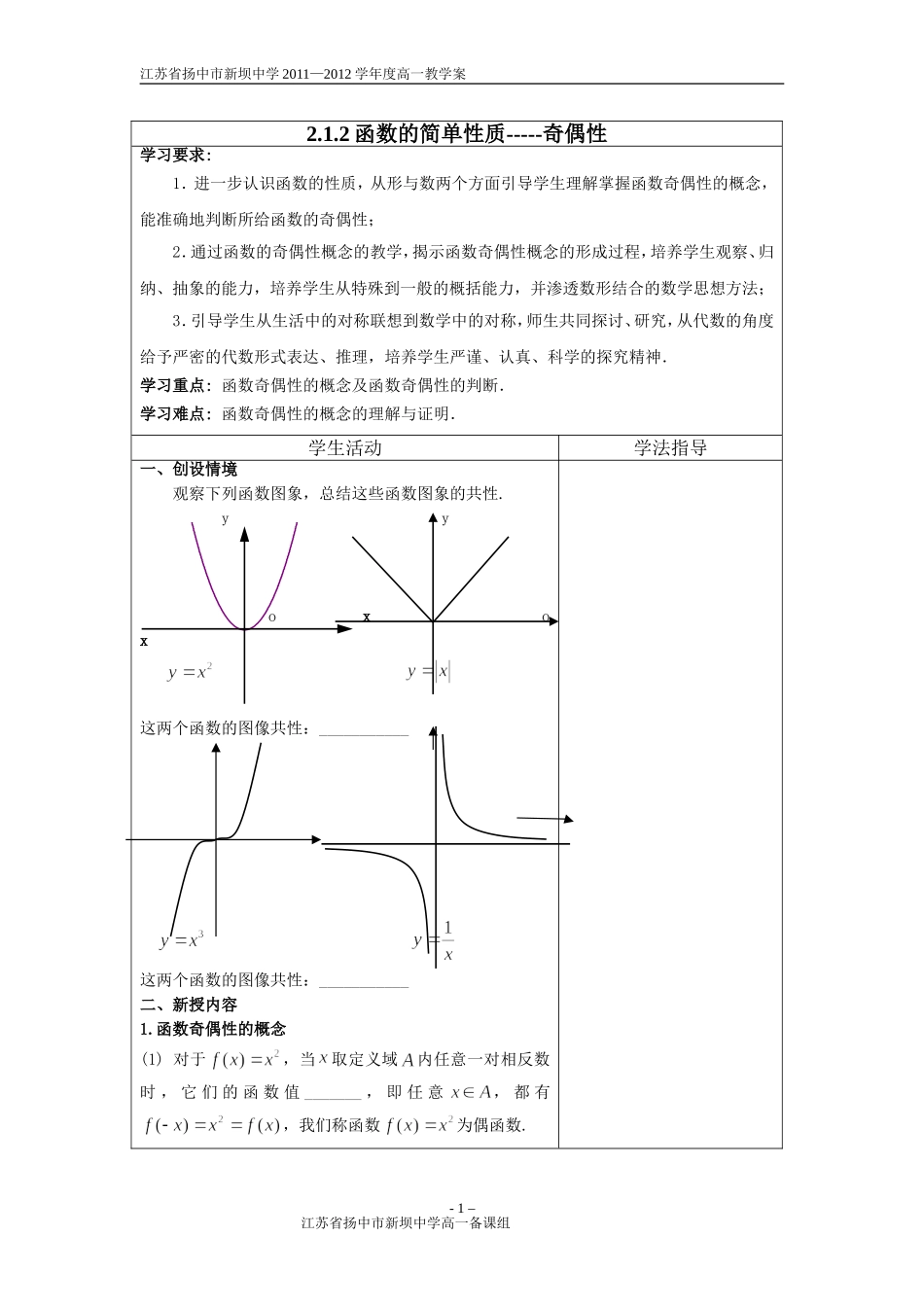
江苏省扬中市新坝中学2011—2012学年度高一教学案2.1.2函数的简单性质-----奇偶性学习要求:1.进一步认识函数的性质,从形与数两个方面引导学生理解掌握函数奇偶性的概念,能准确地判断所给函数的奇偶性;2.通过函数的奇偶性概念的教学,揭示函数奇偶性概念的形成过程,培养学生观察、归纳、抽象的能力,培养学生从特殊到一般的概括能力,并渗透数形结合的数学思想方法;3.引导学生从生活中的对称联想到数学中的对称,师生共同探讨、研究,从代数的角度给予严密的代数形式表达、推理,培养学生严谨、认真、科学的探究精神.学习重点:函数奇偶性的概念及函数奇偶性的判断.学习难点:函数奇偶性的概念的理解与证明.学生活动学法指导一、创设情境观察下列函数图象,总结这些函数图象的共性.yyoxox这两个函数的图像共性:___________这两个函数的图像共性:___________二、新授内容1.函数奇偶性的概念(1)对于,当取定义域内任意一对相反数时,它们的函数值_______,即任意,都有,我们称函数为偶函数.-1–江苏省扬中市新坝中学高一备课组江苏省扬中市新坝中学2011—2012学年度高一教学案(2)对于,当取定义域内任意一对相反数时,它们的函数值_______,即任意,都有,我们称函数为奇函数.一般地:设函数的定义域为.若对于任意的,都有____________,则称函数为偶函数;若对于任意的,都有____________,则称函数为奇函数.如果函数是奇函数或偶函数,我们就说函数具有奇偶性.几个注意点:(1)对定义中“任意”的理解;(2)具有奇偶性的函数的一个必不可少的条件:定义域在数轴上所表示的区间关于原点对称;(3)函数的奇偶性可分为:奇函数,偶函数,非奇非偶函数,既奇且偶函数试一试:(定义在上的函数,判断下列命题是否正确?)(1)若,则函数是偶函数;()(2)若,则函数不是偶函数;()(3)若,则函数不是奇函数;()(4)函数是一个偶函数;()(5)函数是一个既奇且偶函数.()2.奇函数与偶函数的图像特征(1)如果一个函数是奇函数,则这个函数的图象关于___________对称;反之如果一个函数的图像关于_________对称,则这个函数是奇函数.(2)如果一个函数是偶函数,则这个函数的图象关于___________对称;反之如果一个函数的图像关于_________对称,则这个函数是偶函数.三、例题选讲例1.判定下列函数是否为偶函数或奇函数:-2–江苏省扬中市新坝中学高一备课组江苏省扬中市新坝中学2011—2012学年度高一教学案(1)f(x)=x2-1;(2)f(x)=2x;(3)f(x)=2|x|;(4)f(x)=(x-1)2.判断函数奇偶性的步骤:_____________________小结:1.判断函数是否为偶函数或奇函数,首先判断函数的定义域是否关于原点对称,如函数f(x)=2x,x∈[-1,3]就不具有奇偶性;再用定义.2.判定函数是否具有奇偶性,一定要对定义域内的任意的一个x进行讨论,而不是某一特定的值.如函数f(x)=x2-x-1,有f(1)=-1,f(-1)=1,显然有f(-1)=-f(1),但函数f(x)=x2-x-1不具有奇偶性,再如函数f(x)=x3-x2-x+2,有f(-1)=f(1)=1,同样函数f(x)=x3-x2-x+2也不具有奇偶性.例2判断函数f(x)=x3+5x的奇偶性.练习:1.判断下列函数的奇偶性:(1)f(x)=x+;(2)f(x)=x2+;(3)f(x)=;(4)f(x)=.2.已知奇函数f(x)在y轴右边的图象如图所示,试画出函数f(x)在y轴左边的图象.-3–江苏省扬中市新坝中学高一备课组xyO江苏省扬中市新坝中学2011—2012学年度高一教学案3.函数的图象是否关于某条直线对称?它是否为偶函数?4.证明函数在R上是奇函数。课堂检测:判断下列函数奇偶性(1)(2)(3);(4);(5)(6)本课小结:___________________________________教学反思-4–江苏省扬中市新坝中学高一备课组