向量的数量积VIP免费

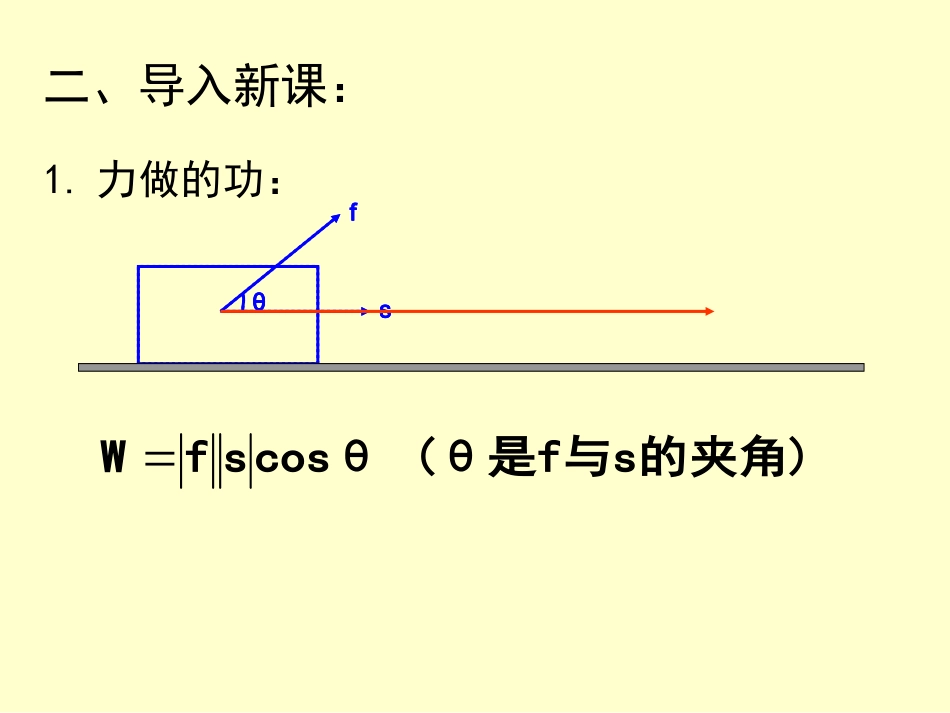
向量的数量积(一)一、复习：前面已经学过：向量的加法、减法、实数与向量的乘法。它们有一个共同的特点，即运算的结果还是向量。二、导入新课：1.力做的功：sfθ(θ是f与s的夹角)cosθsfWsfθ2.向量夹角的概念：的夹角。b,a称为两向量成的角的始点重合，两向量所b,a定义：两向量baθ=001.平行且方向相同2.平行且方向相反θ=1800ab3.不平行时θbaabθπ],[0两向量所成角θ3.向量数量积定义：ba记为：的数量积(内积)。b,a叫做向量cosθbaπ])，把，[0(θ夹角为θb,a设两个向量cosθbaba即：。0与任何向量的数量积为0规定：(1)两个向量的数量积是一个实数，不是向量。其符号由cosθ的符号所确定。的形式。ba或ba成。不能错误地写ba积记为：(2)两个向量的数量注意：可能为零。.因为cosθ0b或0a0不能推出ba(3)若)(请同学们举反倒cb不能推出caba(4)若.BCAB,ACAB求：边长为6的正三角形例1：已知ΔABC是ABC4.一个向量在另一个向量上的投影：的方向上的投影。a在向量b夹角)叫做向量b与acosθ(θ是b定义：把abOAθBB1B1BabAθOabAOBθ注意投影为正；(2)当θ为锐角时，负；当θ为钝角时，投影为时，投影为0；2π当θ＝;b当θ＝0时，投影为.b当θ＝π时，投影为（1）投影是一个数量，不是向量。5.向量数量积的几何意义：cosθ的乘积。b向上的投影的方a在向量b与另一个向量a的模a量的数量积是其中一个向b,a两个向量6.向量数量积运算性质：0＝a＝0时，aa当且仅当0aaaa(1)22abba(2))baλ()b(λab)a(3)(λcaba)cb(a(4)性质(4)推广：2220bba2a)ba.(1220ba)ba)(ba.(32220bba2a)ba.(222)ba()ba例2：化简：(b2a3，求3π夹角为b与a且,3b,2a例3：已知7.两个向量垂直的条件：0ba要条件是：两个非零向量垂直的充实数k的值。垂直，求ba与kbak,4b,2a例4：已知.c求,b2a3c(2)若)ba(a(1)求：1,ba且,ba3ba例5：已知