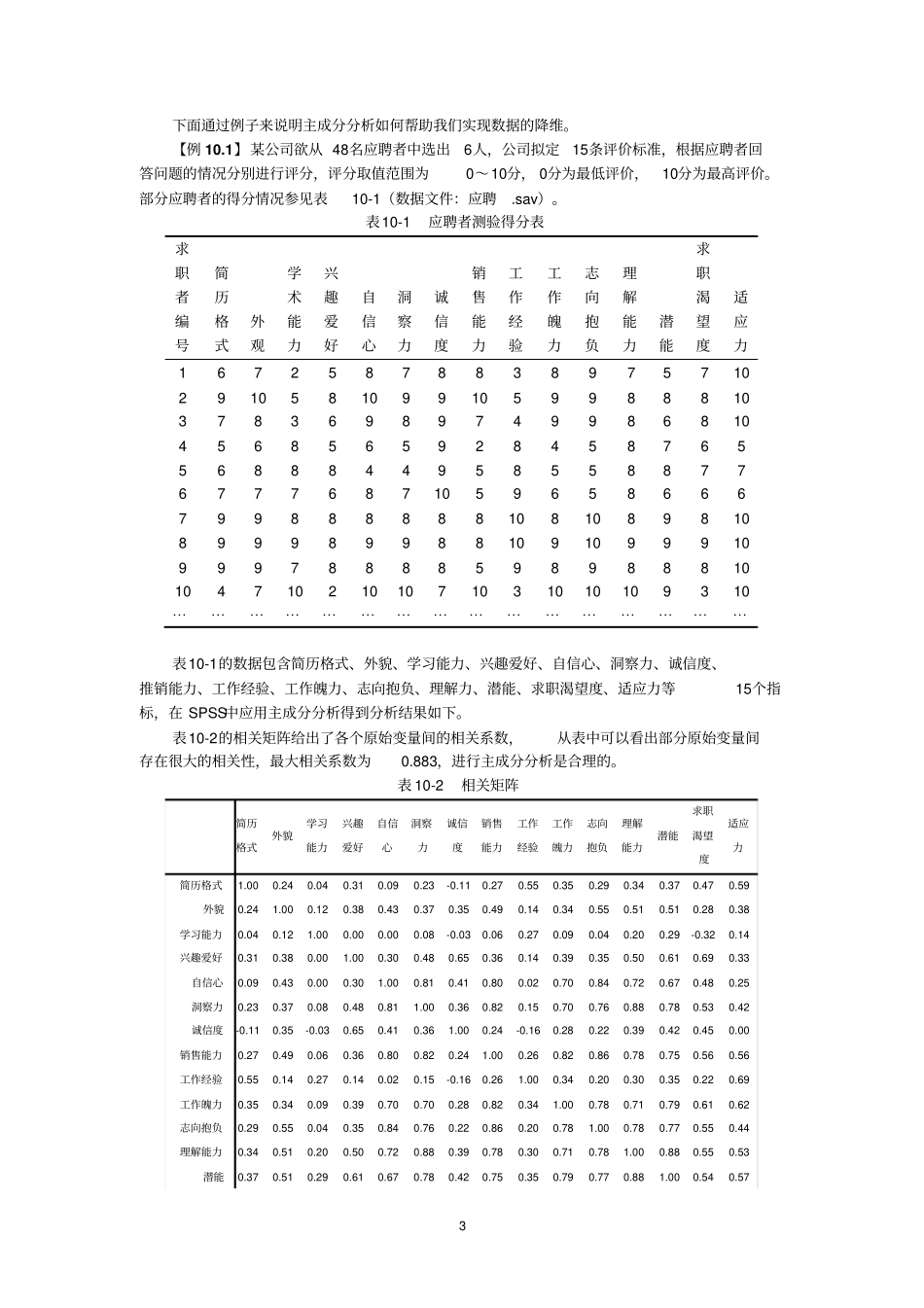
1第十章主成分分析与因子分析一个有经验的裁缝加工一件上衣,需要测量上体长、手臂长、胸围、颈围、肩宽、腰围等14个指标,但在批量生产中,测量每个人的14个指标是不可能的,怎么办呢?人们发现,这14个指标之间具有相关性,如果从这些指标中构造出少数几个指标,只要根据这少数的几个主要指标加工出的上衣就能适合大多数人的体型,即这少数几个指标充分把握了上衣的主要特征。事实上,采用主成分分析和因子分析便能找到两个不相关的指标“型和号”,根据这两个指标加工出的上衣,特体除外,95%以上的人都能穿。从14个指标中构造出两个不相关的指标的过程就称为降维。在现实中类似的降维事例是很多的,在统计学中主要利用因子分子和主成分分析实现对数据的降维处理。这一章我们将介绍因子分析和主成分分析如何实现降维,以及在SPSS中如何实现这两种方法。第一节主成分分析一、主成分分析的基本思想1.基本思想和数学模型在对某一事件进行研究时,常常会涉及到与此相关的多个变量,而这些变量之间往往存在着相关性,很多的变量以及变量间的相关性大大增加了研究的复杂程度。主成分分析就是在解决上述问题过程中产生的,目的在于用少数几个不相关的主成分来代表原来的多个变量,以方便我们对问题的分析。所谓的主成分就是指多个变量的线性组合,不同的主成分之间相互无关。假设有n个样品,每个样品有p个变量分别为pXXX,...,,21,则主成分的个数最多可以有p个,用公式表示为:ppiiiiXaXaXaF...2211pi,...,2,1。方程应满足下列条件:(1)1...22221piiiaaa。(2)iF与jF(pjiji,...,2,1,;)不相关。(3)1F到pF方差依次递减。第一个条件对系数加以限制使得方差不会任意增大。如果不对系数加以限制,方差可以趋于无穷大就变得没有意义了,同时第一个条件也使得每个主成分都是原始变量的凸函数。第二个条件也是主成分分析的灵魂所在,进行主成分分析的依据就是原始变量间的相关性,用不相关的主成分表达相关的原始变量的信息来实现降维,也是在提取主成分时不会提取重复的信息。第三个条件中每个主成分的方差衡量了每个主成分所能表示的原始变量信息的多少,1F到pF方差依次递减为提取主成分提供了方便。在提取主成分时,可以根据方差的大小确2定主成分的个数。这个条件可以保证被提取的每个主成分都比不被提取的主成分包含更多的原始变量信息,以保证在降维的同时最大限度的提取原始信息。2.主成分的几何意义通过前面的介绍,了解到主成分在代数观点上就是原始变量的线性组合,而在几何上可表示为是对原始变量进行线性变换,从而实现以较少的维度表达大部分原始变量的信息。为了方便在坐标中表现降维的几何过程,下面以二元为例来说明主成分的几何意义。设有n个样品,每个样品有两个变量1X和2X,这样画出这n个样品的散点图如图10-1。图10-1二维空间主成分示意图从图10-1可以看到数据都集中在椭圆的区域内。在水平轴1X和2X的两个方向上,我们看到数据点是很分散的,把原始变量作线性变换就相当于把原坐标轴进行旋转,把坐标轴旋转到与椭圆的长短轴平行的1F和2F方向上。相对于长轴如果短轴上的波动可以忽略时,就可以只用长轴的变量来表示原始两个变量的信息,即:把原来的1X和2X两个变量信息只用1F来表示,也就完成了降维的过程。一种极端的情况是:如果短轴趋近于0时,只用一个长轴变量就可以提取几乎所有的原始信息。在多元的情况下是类似于二元的多元空间中椭球体的主轴问题,计算要比二元的情况复杂的多,但思想是相同的,在计算机的辅助下可以很简单的实现对多元的降维,具体的实施在下面的软件实现中会有详细的介绍。二、主成分分析的步骤和结果分析主成分可以按以下步骤计算得出:计算原始变量的相关系数矩阵R;计算相关系数矩阵R的特征值,并按从大到小的顺序排列,记为p21;计算特征值对应的特征向量,即为主成分F1到Fp相应的系数。把原始变量的值代入主成分表达式中,可以计算出主成分得分。注意在计算主成分得分时需要先对原始变量进行标准化。得到各主成分得分后,可以把各个主成分看作新的变量代替原始变量,从而达到降维的目的。对于第k个主成分,其对方差的贡献率为piik1。...