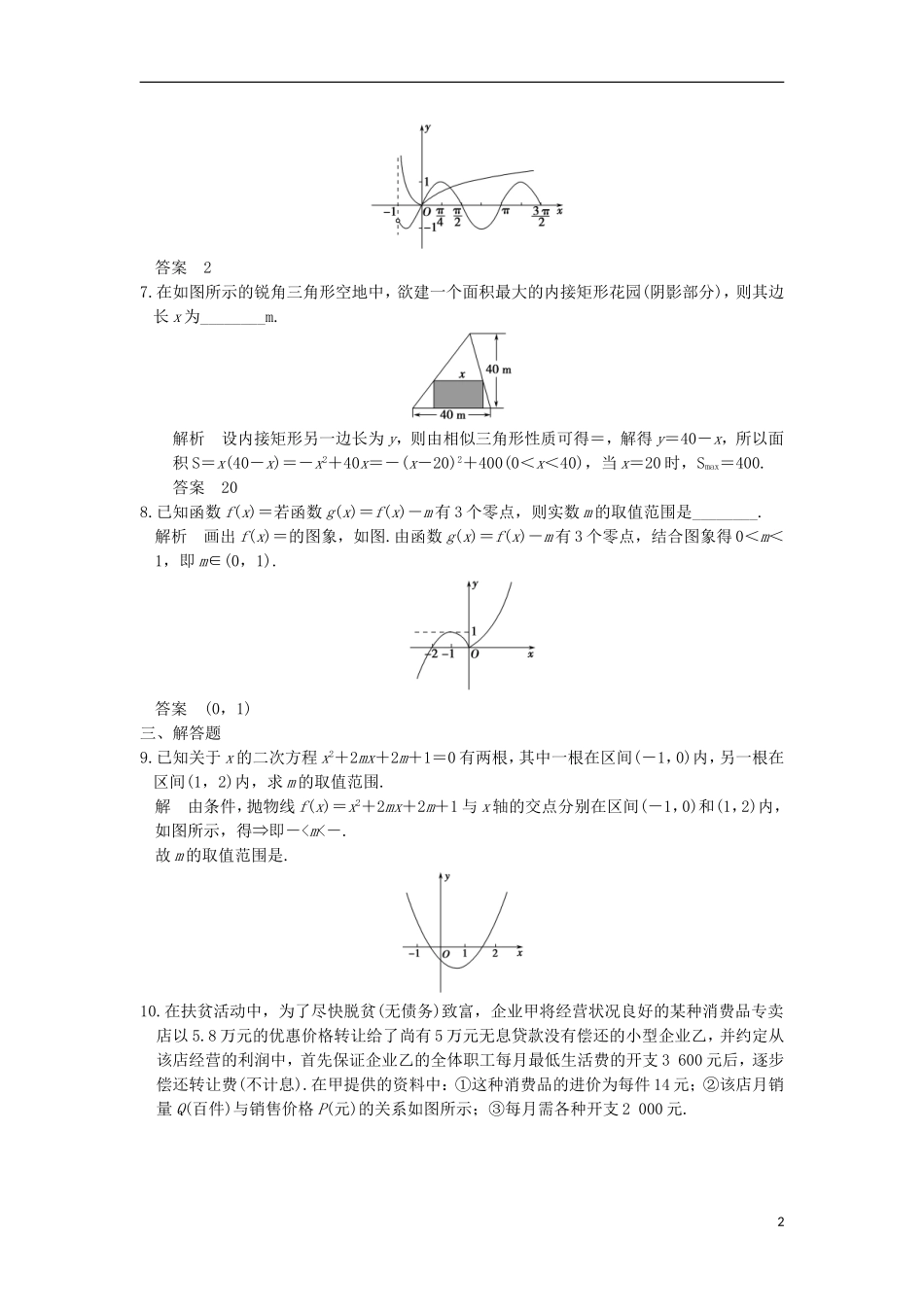
【创新设计】(浙江专用)2017版高考数学一轮复习第二章函数概念与基本初等函数Ⅰ第8讲函数的应用练习基础巩固题组(建议用时:40分钟)一、选择题1.(2016·厦门模拟)函数f(x)=2x-的零点所在的大致区间是()A.B.C.D.解析由题意知函数f(x)在(0,+∞)上单调递增,且f=2-2<0,f(1)=21-1>0,所以函数的零点在区间内.答案B2.若函数f(x)=ax+b有一个零点是2,那么函数g(x)=bx2-ax的零点是()A.0,2B.0,C.0,-D.2,-解析由已知得b=-2a,所以g(x)=-2ax2-ax=-a(2x2+x).令g(x)=0,得x1=0,x2=-.答案C3.(2015·台州二模)已知函数f(x)=-log3x,若x0是函数y=f(x)的零点,且0<x1<x0,则f(x1)的值()A.恒为正值B.等于0C.恒为负值D.不大于0解析注意到函数f(x)=-log3x在(0,+∞)上是减函数,因此当0<x1<x0时,有f(x1)>f(x0).又x0是函数f(x)的零点,因此f(x0)=0,所以f(x1)>0,即此时f(x1)的值恒为正值,选A.答案A4.某企业投入100万元购入一套设备,该设备每年的运转费用是0.5万元,此外每年都要花费一定的维护费,第一年的维护费为2万元,由于设备老化,以后每年的维护费都比上一年增加2万元.为使该设备年平均费用最低,该企业需要更新设备的年数为()A.10B.11C.13D.21解析设该企业需要更新设备的年数为x,设备年平均费用为y,则x年后的设备维护费用为2+4+…+2x=x(x+1),所以x年的平均费用为y==x++1.5(x∈N*),由基本不等式得y=x++1.5≥2+1.5=21.5,当且仅当x=,即x=10时取等号,所以选A.答案A5.若函数f(x)=ax2-x-1有且仅有一个零点,则实数a的取值为()A.0B.-C.0或-D.2解析当a=0时,函数f(x)=-x-1为一次函数,则-1是函数的零点,即函数仅有一个零点;当a≠0时,函数f(x)=ax2-x-1为二次函数,并且仅有一个零点,则一元二次方程ax2-x-1=0有两个相等实根.∴Δ=1+4a=0,解得a=-.综上,当a=0或a=-时,函数仅有一个零点.答案C二、填空题6.(2015·湖北卷)函数f(x)=4cos2cos-2sinx-|ln(x+1)|的零点个数为________.解析f(x)=2(1+cosx)sinx-2sinx-|ln(x+1)|=sin2x-|ln(x+1)|,x>-1,函数f(x)的零点个数即为函数y=sin2x与y=|ln(x+1)|(x>-1)的图象的交点个数.分别作出两个函数的图象,如图,可知有两个交点,则f(x)有两个零点.1答案27.在如图所示的锐角三角形空地中,欲建一个面积最大的内接矩形花园(阴影部分),则其边长x为________m.解析设内接矩形另一边长为y,则由相似三角形性质可得=,解得y=40-x,所以面积S=x(40-x)=-x2+40x=-(x-20)2+400(0<x<40),当x=20时,Smax=400.答案208.已知函数f(x)=若函数g(x)=f(x)-m有3个零点,则实数m的取值范围是________.解析画出f(x)=的图象,如图.由函数g(x)=f(x)-m有3个零点,结合图象得0<m<1,即m∈(0,1).答案(0,1)三、解答题9.已知关于x的二次方程x2+2mx+2m+1=0有两根,其中一根在区间(-1,0)内,另一根在区间(1,2)内,求m的取值范围.解由条件,抛物线f(x)=x2+2mx+2m+1与x轴的交点分别在区间(-1,0)和(1,2)内,如图所示,得⇒即-