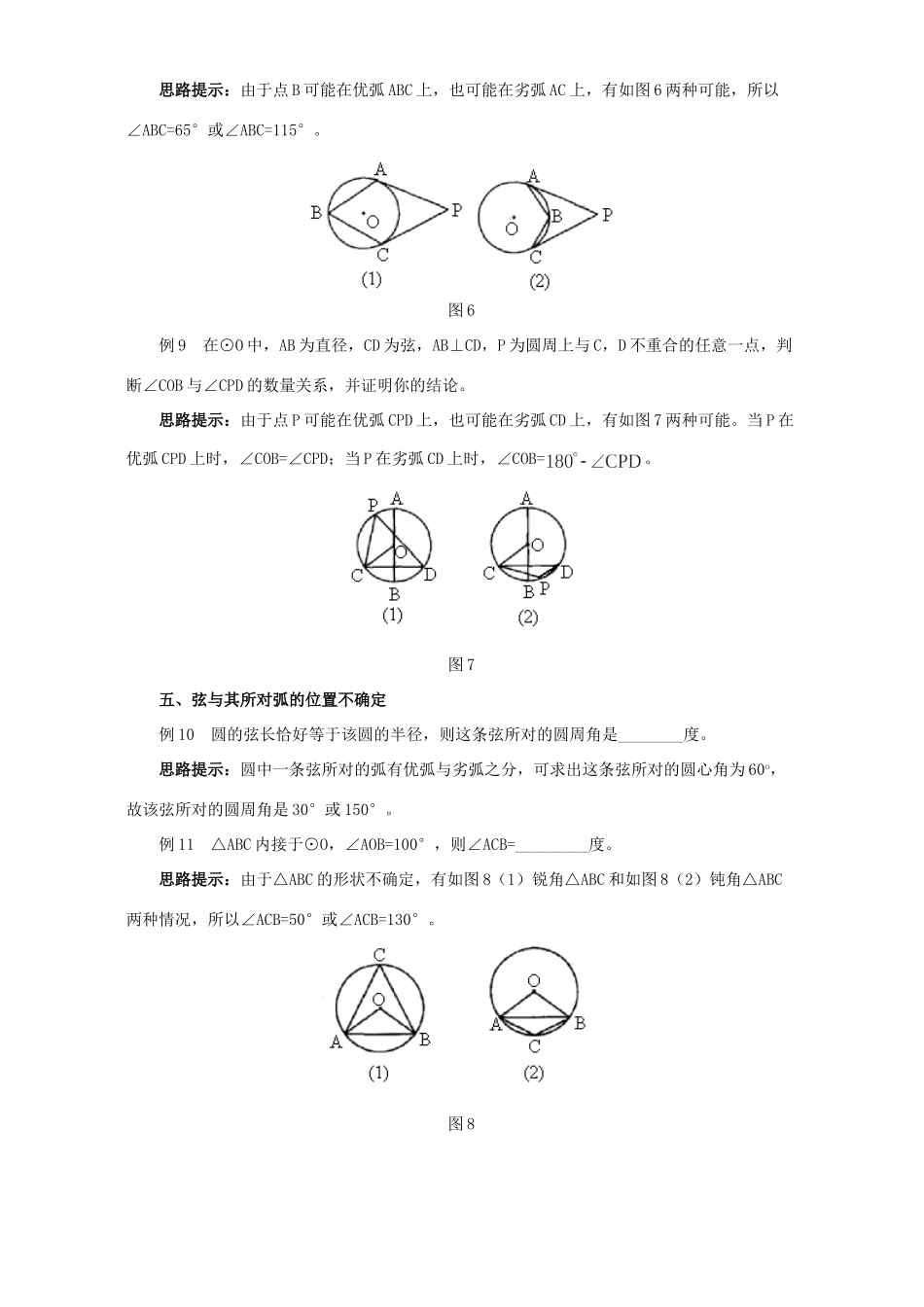
初中数学关注圆中两解问题考察近年来各省市中考试题发现,有关圆的两解问题经常出现。这类题目重在考查同学们对基础知识的掌握与运用情况,这有利于培养严谨的逻辑思维能力。如果解题时考虑不严密,形成思维定势,就会漏解。现就圆中常见的两解问题举例分析,以期引起重视。一、点与圆的位置不确定例1在同一平面内,点P到⊙O的最长距离为8cm,最短距离为2cm,则⊙O的半径为___________。思路提示:由于点P与⊙O的位置关系有如图1两种可能,所以⊙O的半径应为5cm或3cm。图1例2⊙O的直径为6cm,如果直线a上的一点C到点O的距离为3cm,则直线a与⊙O的位置关系是_________。思路提示:题中只涉及点C到圆心的距离,并非是圆心到直线的距离,有如图2两种可能,所以直线a与⊙O的位置关系是相切或相交。图2二、圆心与弦的位置不确定例3⊙O的半径为5cm,弦AB//CD,AB=6cm,CD=8cm,求AB与CD之间的距离。思路提示:圆心O与两平行弦的位置有如图3两种可能。利用垂径定理可求出OE=4cm,OF=3cm,所以AB与CD之间的距离为1cm或7cm。图3例4⊙O1与⊙O2相交于A、B两点,⊙O1的半径为10,⊙O2的半径为17,公共弦AB=16,求两圆的圆心距。思路提示:对两圆相交问题,一些考生往往只考虑两圆的圆心在公共弦两侧的情况,即图4(1)的情况,很容易遗漏图4(2)的情况,所以正确答案是=21或=9。图4例5⊙O的半径为1cm,弦,,则∠BAC=________。思路提示:由于弦AB和CD可能在圆心的同侧,也可能在圆心的异侧,有如图5两种可能。根据垂径定理及解直角三角形知识可求出∠CAO=45°和∠BAO=30°,从而可知∠BAC=15°或∠BAC=75°。图5三、圆与圆的位置不确定例6两圆相切,圆心距是10cm,其中一圆的半径为4cm,则另一圆的半径是_____。思路提示:两圆相切有内切和外切两种情况,所以另一圆的半径为6cm或14cm。例7⊙O1的半径为2cm,⊙O2的半径为5cm,两圆没有公共点,则两圆的圆心距d的取值范围为___________。思路提示:两圆没有公共点,则⊙O1与⊙O2有外离或内含两种情况,外离时,d>7cm;内含时,0cm≤d<3cm。四、点在弧上的位置不确定例8PA,PC分别切⊙O于A,C两点,B为⊙O上与A,C不重合的点,若∠P=50°,则∠ABC=_________度。思路提示:由于点B可能在优弧ABC上,也可能在劣弧AC上,有如图6两种可能,所以∠ABC=65°或∠ABC=115°。图6例9在⊙O中,AB为直径,CD为弦,AB⊥CD,P为圆周上与C,D不重合的任意一点,判断∠COB与∠CPD的数量关系,并证明你的结论。思路提示:由于点P可能在优弧CPD上,也可能在劣弧CD上,有如图7两种可能。当P在优弧CPD上时,∠COB=∠CPD;当P在劣弧CD上时,∠COB=。图7五、弦与其所对弧的位置不确定例10圆的弦长恰好等于该圆的半径,则这条弦所对的圆周角是________度。思路提示:圆中一条弦所对的弧有优弧与劣弧之分,可求出这条弦所对的圆心角为60o,故该弦所对的圆周角是30°或150°。例11△ABC内接于⊙O,∠AOB=100°,则∠ACB=_________度。思路提示:由于△ABC的形状不确定,有如图8(1)锐角△ABC和如图8(2)钝角△ABC两种情况,所以∠ACB=50°或∠ACB=130°。图8