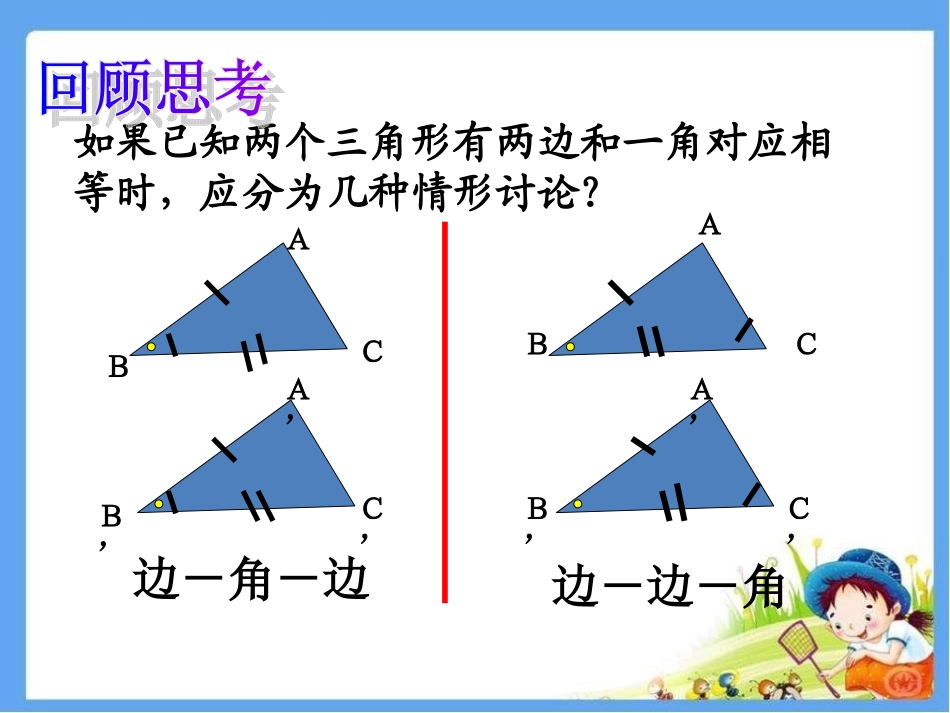
12.2三角形全等的判定一(SAS)AEFBC全等三角形的性质是什么?对应边相等;对应角相等。如:△ABC≌△DEF,可以写出以下推理: △ABC≌△DEF(已知)∴AB=DE,BC=EF,AC=DF(全等三角形对应边相等)∠A=∠D,∠B=∠E,∠C=∠F(全等三角形对应角相等)ABCDEF如果已知两个三角形有两边和一角对应相等时,应分为几种情形讨论?边-角-边边-边-角AAA’A’BB’BB’CCC’C’做一做:画△ABC,使AB=3cm,AC=4cm.画法:1.画线段AB=3cm;3.在射线AM上截取AC=4cm;这样画出来的三角形与同桌所画的三角形进行比较,它们互相重合吗?若再加一个条件,使∠A=45°,画出△ABC.2.画∠MAB=45°;4.连接BC.△ABC就是所求的三角形.把你们所画的三角形剪下来与同桌所画的三角形进行比较,它们能互相重合吗?探究用几何语言表达为:在△ABC与△A`B`C`中∴△ABCA`B`C`≌△(SAS)如果两个三角形有两边及其夹角分别对应相等,那么这两个三角形全等。简写成“边角边”或““SSAS”AS” AB=A`B`∠B=B`∠BC=B`C`ABCA`B`C`如图△ABC和△DEF中,AB=DE=3㎝,∠B=E=30∠0,BC=EF=5㎝,它们完全重合吗?△ABCDEF≌△吗?为什么?3㎝5㎝300ABC3㎝5㎝300DEF它们完全重合,即△ABCDEF≌△.根据边角边.是不是两条边和一个角对应相等的两个三角形就一定全等?你能举例说明吗?以3cm、4cm为三角形的两边,长度3cm的边所对的角为45°,情况又怎样?动手画一画,你发现了什么?4cm3cm45°A3cm步骤:1.画一线段AC,使它等于4cm;2.画∠CAM=45°;3.以C为圆心,3cm长为半径画弧,交AM于点B;4.连结CB.△ABC与△AB'C就是所求做的三角形.显然:△ABC与△AB'C不全等BB’MMC结论:两边及其一边所对的角相等,两个三角形不一定全等.分别找出各题中的全等三角形ABC40°40°DEF(1)DCAB(2)△ABC≌△EFD根据“SAS”△ADC≌△CBA根据“SAS”平行四边形ABCD如图,下列哪组条件不能判定△ABC≌△DEF()ABCDEFAB=DEA、∠A=∠DAC=DFAC=DFC、∠C=∠FBC=EFAB=DEB、∠B=∠EBC=EFAC=DFD、∠B=∠EBC=EFD利用边角边判断两个三角形全等时,角一定是两边的夹角。已知:如图,AB=CB,∠1=∠2,△ABD和△CBD全等吗?为什么?分析:△ABD≌△CBD边AB=CB(已知)角∠1=∠2(已知)边BD=BD(公共边)ABCD(SAS)解:在△ABD和△CBD中, AB=CB(已知)∠ABD=CBD(∠已知)BD=BD(公共边)∴△ABDCBD(SAS)≌△12B2B如图,有一池塘,要测池塘两端如图,有一池塘,要测池塘两端AA、、BB的距离,的距离,可在平地上取一个可直接到达可在平地上取一个可直接到达AA和和BB的点的点CC,,连结连结ACAC并延长至并延长至DD使使CD=CACD=CA,连结,连结BCBC并延长并延长至至EE使使CE=CBCE=CB,连结,连结EDED,那么量出,那么量出DEDE的长,的长,就是就是AA、、BB的距离,为什么?的距离,为什么?解决问题解决问题BBAADDEECC证明:在△证明:在△ABCABC和△和△DECDEC中,中,AC=DC(AC=DC(已知已知))∠∠ACB=∠DCE(ACB=∠DCE(对顶角相等对顶角相等))BC=EC(BC=EC(已知已知))∴△∴△ABC≌△DECABC≌△DEC((SASSAS))∴∴AB=DEAB=DE((全等三角形的对应边相等全等三角形的对应边相等))已知:如图,AD∥BC,AD=CB.求证:△ADC≌△CBAABCD12证明: AD∥BC∴∠1=∠2(两直线平行,内错角相等)在△ADC和△CBA中 AD=CB(已知)∠1=∠2(已证)AC=CA(公共边)∴△ADC≌△CBA(SAS)已知:如图,AD∥BC,AD=BC,AE=CF.求证:△AFD≌△CEBADEFBC AD∥BC∴∠A=∠C(两直线平行,内错角相等)证明: AE=CF∴AE+EF=CF+EF即AF=CE在△ADF和△CEB中 AD=CB(已知)∠A=∠C(已证)AF=CE(已证)∴△AFD≌△CEB(SAS)已知:如图,AB=AC,AD=AE.求证:△ABE≌△ACDACDBEA证明:在△ABE和△ACD中 AB=AC(已知)∠A=∠A(公共角)AD=AE(已知)∴△ABE≌△ACD(SAS)已知:如图,AB=AC,AD=AE,∠1=∠2.求证:△ADB≌△ACE1ACE2ABD证明: ∠1=∠2(已知)∴∠1+∠BAE=∠2+∠BAE,即∠CAE=∠BAD在△ADB和△ACE中 AB=AC(已知)∠CAE=∠BAD(已证)AD=AE(已知)∴△ADB≌△ACE(SAS)ABCDO如图AC与BD相交于点O,已知OA=OC,OB=OD,说明△AOBCOD≌△的理由。解:在△AOB和△COD中 OA=OC(已知)∠AOB=∠COD(对顶角)OB=OD(已知)∴...