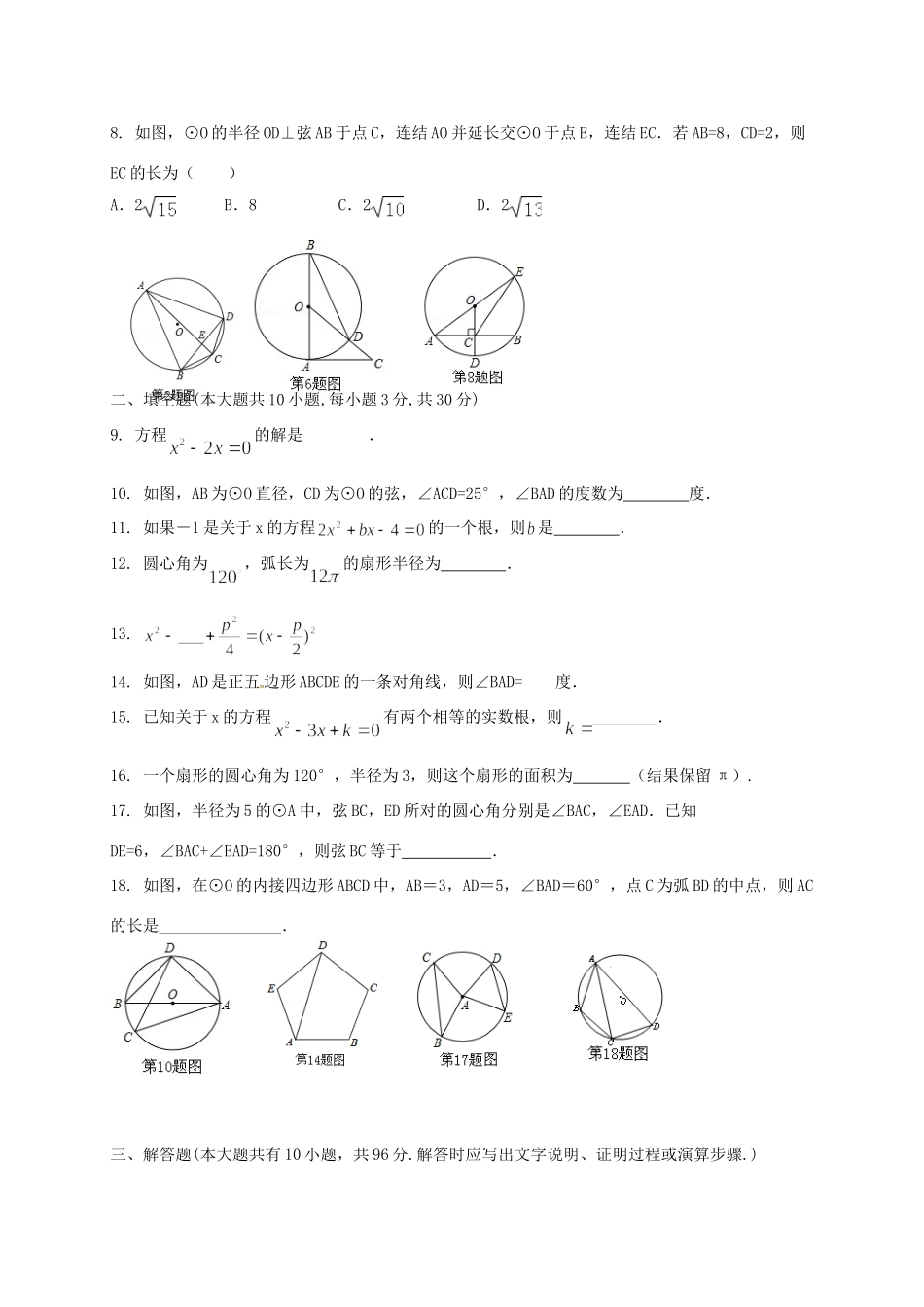
九年级1O月阶段测试数学试题(考试时间:120分钟试卷满分:150分考试形式:闭卷)一、选择题(本大题共8小题,每小题3分,共24分)1.下列方程中一定是关于x的一元二次方程的是()A.B.C.D.2.如图,点A,B,C,D都在⊙O上,AC,BD相交于点E,则∠ABD=()A.∠ACDB.∠ADBC.∠AEDD.∠ACB3.将方程左边配方后,正确的是()A.B.C.D.4.在Rt△ABC中,∠C=90°,AC=12,BC=5,将△ABC绕边AC所在直线旋转一周得到圆锥,则该圆锥的侧面积是()A.25πB.65πC.90πD.130π5.关于x的一元二次方程kx2+2x-1=0有两个不相等的实数根,则k的取值范围是()A.k>-1B.k>1C.k≠0D.k>-1且k≠06.如图,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD,∠C=40°.则∠ABD的度数是()A.30°B.25°C.20°D.15°7.某商品原价200元,连续两次降价a%后售价为148元,下面所列方程正确的是()A.200(1+a%)2=148B.200(1-a%)2=148C.200(1-2a%)=148D.200(1-a2%)=1488.如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为()A.2B.8C.2D.2二、填空题(本大题共10小题,每小题3分,共30分)9.方程的解是.10.如图,AB为⊙O直径,CD为⊙O的弦,∠ACD=25°,∠BAD的度数为度.11.如果-1是关于x的方程的一个根,则是.12.圆心角为,弧长为的扇形半径为.13.14.如图,AD是正五边形ABCDE的一条对角线,则∠BAD=度.15.已知关于x的方程有两个相等的实数根,则.16.一个扇形的圆心角为120°,半径为3,则这个扇形的面积为(结果保留π).17.如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD.已知DE=6,∠BAC+∠EAD=180°,则弦BC等于.18.如图,在⊙O的内接四边形ABCD中,AB=3,AD=5,∠BAD=60°,点C为弧BD的中点,则AC的长是_______________.三、解答题(本大题共有10小题,共96分.解答时应写出文字说明、证明过程或演算步骤.)19.(本题8分)解方程:(1)解方程:(2)解方程:20.(本题8分)如图,CD是⊙O的直径,点A在DC的延长线上,∠A=20°,AE交⊙O于点B,且AB=OC。(1)求∠AOB的度数.(2)求∠EOD的度数.21.(本题8分)已知关于x的方程(k﹣1)x2﹣(k﹣1)x+=0有两个相等的实数根,求k的值.22.(本题8分)如图所示,在Rt△ABC中,∠C=900,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB、BC分别交于点D、E,求AB和AD的长。23.(本题10分)如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.(1)求证:DP是⊙O的切线;(2)若⊙O的半径为3cm,求图中阴影部分的面积.CABDE24.(本题10分)已知某校去年年底的绿化面积为平方米,预计到明年年底的绿化面积将会增加到平方米,求这两年的年平均增长率。25.(本题10分)如图,在△ABC中,∠C=90°,⊙O是△ABC的内切圆,切点分别为D、E、F.若BD=6,AD=4,求⊙O的半径r.26.(本题10分)如图,已知AB是⊙的直径,AC是⊙的弦,过点C作⊙的切线交BA的延长线于点P,连接BC(1)求证:∠PCA=∠B;(2)已知∠P=40°,AB=12cm,点Q在优弧ABC上,从点A开始逆时针运动到点C停止(点Q与点C不重合),当△ABQ与△ABC的面积相等时,求动点Q所经过的弧长.27.(本题12分)某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用含x的代数式来表示销售量(件)和销售该品牌玩具获得利润(元),并把化简后的结果填写在表格中:销售单价(元)x销售量(件)销售玩具获得利润(元)(2)在(1)问条件下,若商场获得了10000元销售利润,试问该玩具销售单价x应定为多少元?(3)在(1)问条件下,商场有可能获得13000元的销售利润吗?若可能,请求出该玩具销售单价;若不可能,请说明理由。28.(本题12分)如图,形如量角器的半圆O的直径DE=12cm,形如三角板的⊿ABC中,∠ACB=90°,∠ABC=30°,BC=12cm。半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上。设运动时间为t(s)...