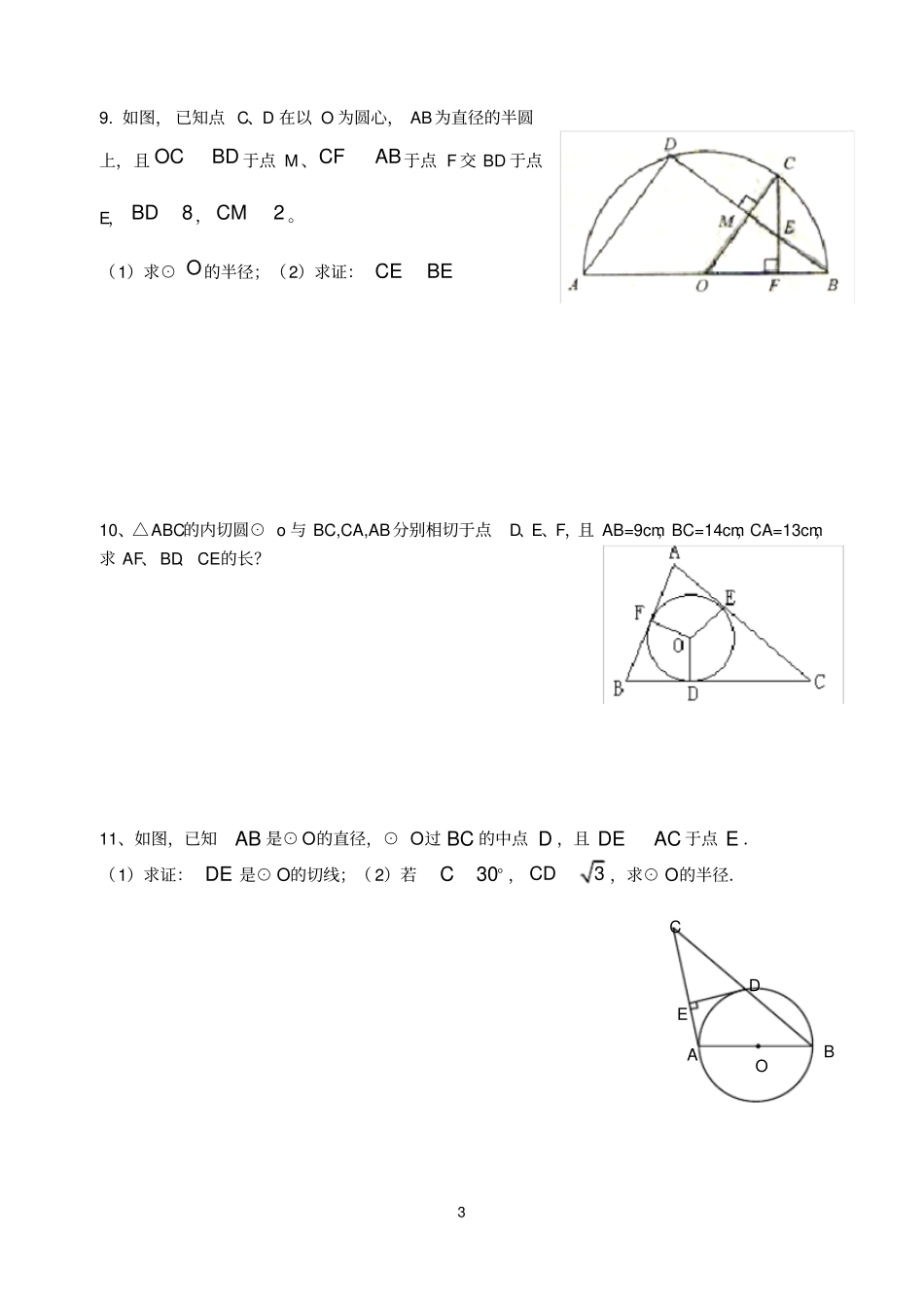
1圆证明专题1.如图,已知在⊙O中,AB=43,AC是⊙O的直径,AC⊥BD于F,∠A=30°.(1)求图中阴影部分的面积;(2)若用阴影扇形OBD围成一个圆锥侧面,请求出这个圆锥的底面圆的半径.2.AB是⊙O的直径,BC是弦,OD⊥BC于E,交弧BC于D。(1)请写出四个正确的结论;(2)若BC=6,ED=2,求⊙O的半径。3.已知:如图,ABC△中,ABAC,以AB为直径的⊙O交BC于点P,PDAC于点D.(1)求证:PD是⊙O的切线;(2)若1202CABABo,,求BC的值4.如图,在Rt△ABC中,∠B=90°,∠A的平分线交BC于D,E为AB上一点,DE=DC,以D为圆心,以DB的长为半径画圆。求证:(1)AC是⊙D的切线;(2)AB+EB=AC。ABCDOFEOBACDCPBOAD25.已知:⊙O的直径AB和弦CD,且AB⊥CD于E,F为DC延长线上一点,连结AF交⊙O于M。求证:∠AMD=∠FMC。6.已知AB是☉O的直径,AC是弦,CD切☉O于点C,交AB的延长线于点D,120ACDo,10BD.(1)求证:CACD;(2)求☉O的半径.7.ABC△内接于⊙O,点D在半径OB的延长线上,30BCDA°.(1)试判断直线CD与⊙O的位置关系,并说明理由;(2)若⊙O的半径长为1,求由弧BC、线段CD和BD所围成的阴影部分面积(结果保留π和根号).8.如图,PA,PB是⊙O的切线,点A,B为切点,AC是⊙O的直径,∠ACB=70°.求∠P的度数.ABDCOAOCBDOPCBA39.如图,已知点C、D在以O为圆心,AB为直径的半圆上,且BDOC于点M、ABCF于点F交BD于点E,8BD,2CM。(1)求⊙O的半径;(2)求证:BECE10、△ABC的内切圆⊙o与BC,CA,AB分别相切于点D、E、F,且AB=9cm,BC=14cm,CA=13cm,求AF、BD、CE的长?11、如图,已知AB是⊙O的直径,⊙O过BC的中点D,且DEAC于点E.(1)求证:DE是⊙O的切线;(2)若30C°,3CD,求⊙O的半径.AEDOBC4DCBAOCPBAO12.如图,已知AB⊙O是的直径,AC为弦,且平分BAD,ADCD,垂足为D.求证:CD是⊙O的切线。13.如图,AC为⊙O直径,B为AC延长线上的一点,BD交⊙O于点D,∠BAD=∠B=30°(1)求证:BD是⊙O的切线;(2)AB=3CB吗?请说明理由。(选做)14.如图所示,⊙O的半径是4,PA、PB分别与⊙O相切于点A、点B,若PA与PB之间的夹角∠APB=60°,(1)若点C是圆上的一点,试求∠APB的大小;(2)求△ABP的周长.15、如图:AB是⊙O的直径,以OA为直径的⊙O1与⊙O的弦AC相交于D,DE⊥OC,垂足为E。(1)求证:AD=DC(2)求证:DE是的切线(3)如果OE=EC,请判断四边形O1OED是什么四边形,并证明你的结论。ODCAB第21题图5CBOADOPABC16.如图,在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A、与大圆相交于点B。小圆的切线AC与大圆相交于点D,且CO平分∠ACB。(1)试判断BC所在直线与小圆的位置关系,并说明理由;(2)试判断线段AC、AD、BC之间的数量关系,并说明理由;(3)若8cm10cmABBC,,求大圆与小圆围成的圆环的面积。(结果保留π)17.如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于D,过D作DE⊥AC,交AC于E,DE是⊙O的切线吗?为什么?18.如图,AB是⊙O的直径,BC是弦,PA切⊙O于A,OP∥BC,求证:PC是⊙O的切线。EOBCADwww.czsx.com.cn619.如图,OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任一点,BP的延长线交⊙O于点Q,过点Q的⊙O的直线交OA延长线于点R,且RP=RQ(1)求证:直线QR是⊙O的切线;(2)若OP=PA=1,试求RQ的长20、如图,AB是⊙O的直径,∠BAC=45°,AB=BC.(1)、求证:BC是⊙O的切线;(2)、设阴影部分的面积为a,b,⊙O的面积为S,请写出S与a,b的关系式。21.如图,已知AB⊙O是的直径,AC为弦,且平分BAD,ADCD,垂足为D.求证:CD是⊙O的切线;(12分)AOBCD