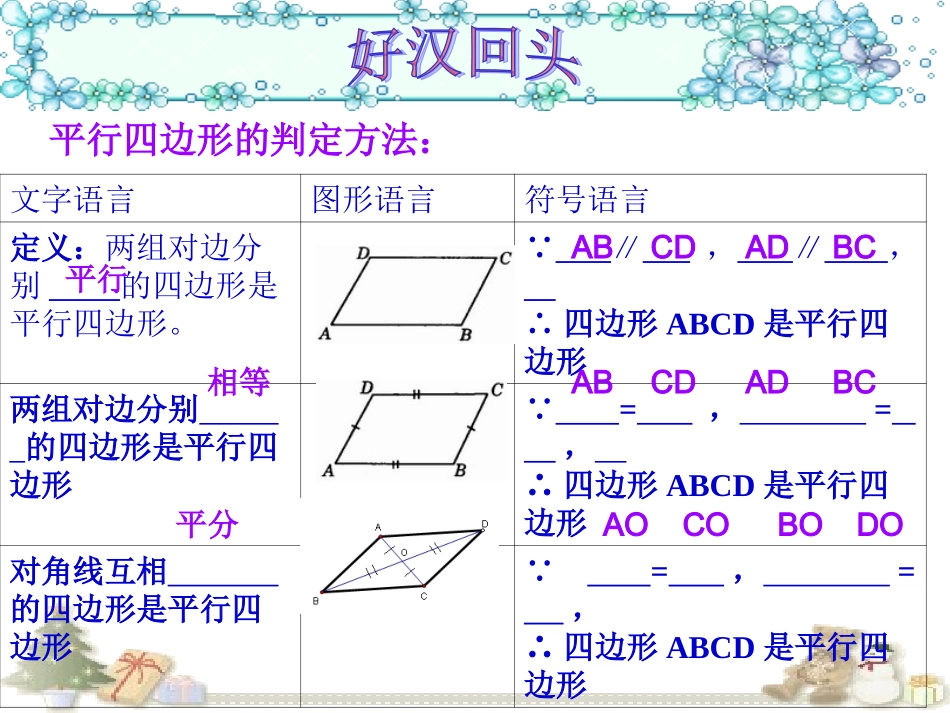
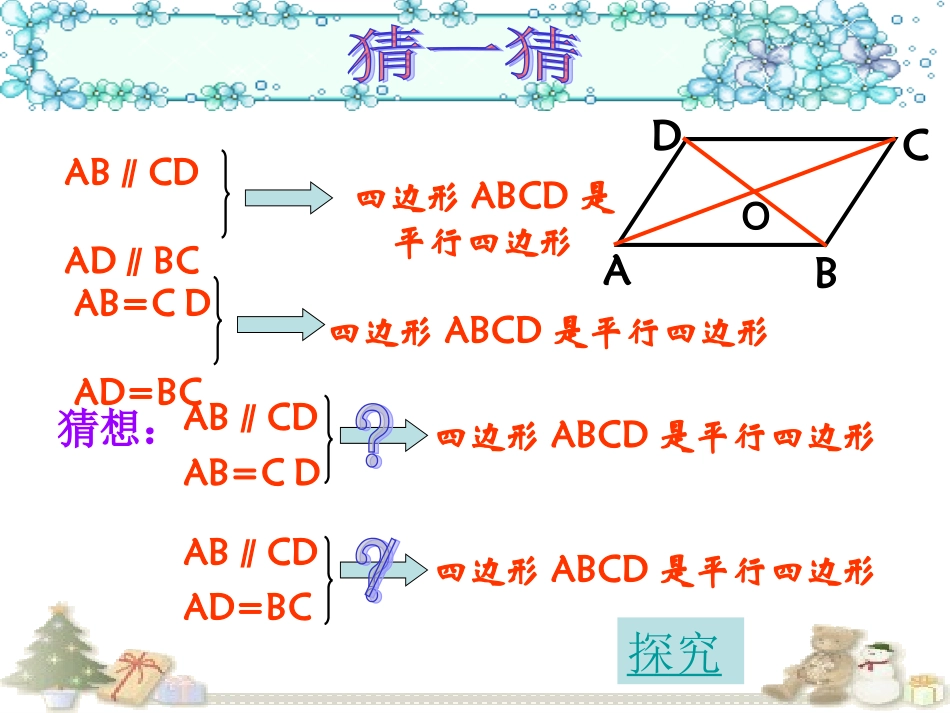
平行四边形的判定方法:文字语言图形语言符号语言定义:两组对边分别的四边形是平行四边形。∵∥,∥,∴四边形ABCD是平行四边形两组对边分别的四边形是平行四边形∵=,=,∴四边形ABCD是平行四边形对角线互相的四边形是平行四边形∵=,=,∴四边形ABCD是平行四边形平行平分相等ABCDADBCABCDADBCAOCOBODOAB∥CDAD∥BC四边形ABCD是平行四边形AB=CDAD=BC四边形ABCD是平行四边形DABCO猜想:AB∥CDAB=CD四边形ABCD是平行四边形AB∥CDAD=BC四边形ABCD是平行四边形探究已知:四边形ABCD中,ABCD∥且AB=CD。求证:四边形ABCD是平行四边形。证明:连结AC∵ABCD∥∴=,在△ABC和△CDA中,∴△ABCCDA≌△()∴=,又AB=CD∴四边形ABCD是平行四边形()∠1∠2ABCDACCA∠1∠2SASBCDA两组对边分别相等的四边形是平行四边形平行四边形判定定理5:一组对边平行且相等的四边形是平行四边形。用几何语言表示:四边形ABCD是平行四边形ABCD//ABCDEF证明:∵ABCD是平行四边形已知:如图求证:四边形EBFD为平行四边形.ABCD,若点E、F分别是AD、BC的中点,∴____∥____,___=____∵E、F分别是AD、BC的中点1212∴ED=_____,BF=_____∴_______=_________又________________∥∴四边形EBFD是平行四边形()ADBCADADBCBCEDBFBFED一组对边平行且相等的四边形是平行四边形。变式1:例题中,E、F分别在AD、BC上移动,使AE=CF,则结论还成立吗?为什么?变式2:ABCD中,若点E、F分别是AD、BC上延长线上的点,当AE、CF满足什么条件时,四边形EBFD为平行四边形?成立。AE=CF3.如图,A、B、E在一直线上,AB=DC,∠C=∠CBE,求证:AD=BC.EBDCA证明:∵∠C=∠CBE,∴ABDC∥又∵AB=DC∴四边形ABCD是平行四边形∴AD=BC平行四边形判定定理4:两组对角分别相等的四边形是平行四边形。用几何语言表示:∠A=∠C四边形ABCD是平行四边形∠B=∠D平行四边形判定定理5:一组对边平行且相等的四边形是平行四边形。用几何语言表示:四边形ABCD是平行四边形ABCD//平行四边形的判定方法:文字语言图形语言符号语言边两组对边分别平行的四边形是平行四边形。∵ABCD,ADBC∥∥∴四边形ABCD是平行四边形两组对边分别相等的四边形是平行四边形。∵AB=CD,AD=BC∴四边形ABCD是平行四边形一组对边平行且相等的四边形是平行四边形。∵ABCD∴四边形ABCD是平行四边形角两组对角分别相等的四边形是平行四边形。∵∠A=C,B=D∠∠∠∴四边形ABCD是平行四边形对角线对角线互相平分的四边形是平行四边形。∵AO=CO,BO=DO,∴四边形ABCD是平行四边形//