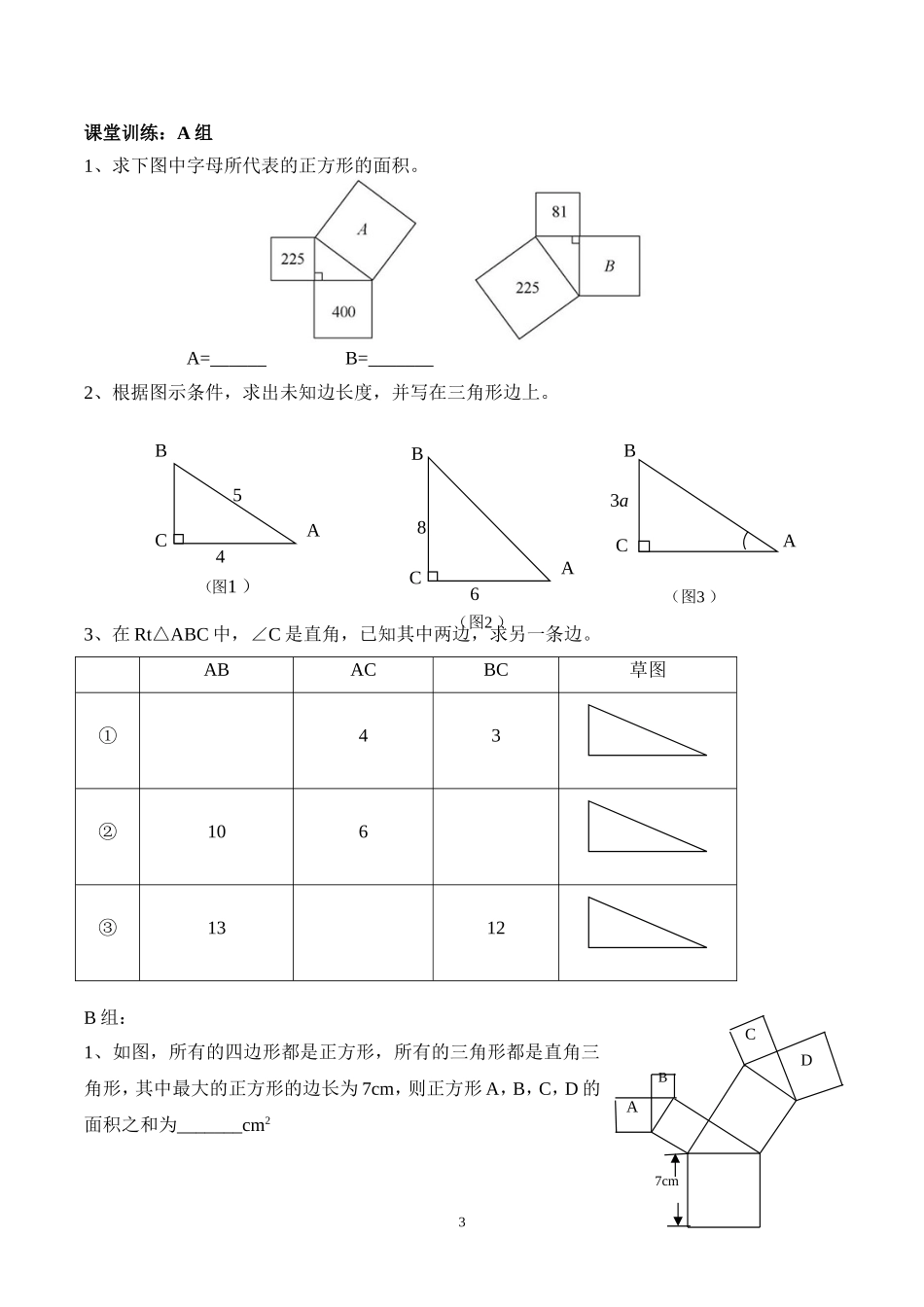
第1课探索勾股定理数学科2013.4学习目标:1、掌握直角三角形三边的数量关系,学会用符号表示勾股定理;2、经历勾股定理的证明过程,体会数形结合的数学思想;3、学会运用勾股定理进行简单的计算。一、知识引入问题:一个门框的尺寸如图所示,一块长8m,宽4.8m的薄木板能否从门框内通过?4m3mDCBA二、观察实验如图所示,以直角三角形的三边为边长,向外作正方形,(1)观察图①:AS=,BS=,CS=。则AS、BS、CS的数量关系是:_________________________________(2)请在图②中仿照上题选择合适的边长画一个直角三角形,然后向外作三个正方形,记为“A”、“B”、“C”。观察三个正方形,可得:AS=,BS=,CS=。则AS、BS、CS的数量关系是:_________________________________三、归纳猜想猜想:如图,Rt△ABC中,∠C=90°,则S1、S2、S3的等量关系为:_______________若直角三角形三边长为a,b,c,则a,b,c的等量关系为:_______________四、验证(拼图验证法)18m4.8m在北京召开的第24届国际数学家大会的会标取材于我国古代数学家赵爽的《赵爽弦图》,它是由四个以a、b为直角边(b>a),以c为斜边的全等的直角三角形与中间的小正方形拼成的一个大正方形,你能通过图中的面积关系得到等式吗?证明:如图所示,用a,b,c表示下列图形的面积得:=__________,=_________∵小正方形的边长为:________,∴=________∴可列等式:即4×_______+________=______化简:勾股定理:直角三角形两直角边的平方和等于斜边的平方.几何语言:如图,在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,则有a2+b2=c2。【例题讲解】例题:一个门框的尺寸如图所示,一块长8m,宽4.8m的薄木板能否从门框内通过?解:如图所示,,AB=3m,BC=4m在中,∴(代入AB、BC的值)∴AC=______()4.8m(填“>”,“=”,“<”)∴木板_____(能/不能)通过门框。小结:(1)使用勾股定理的前提是____________,非直角三角形的三边之间则不存在此种关系.(2)使用勾股定理时,必须分清谁是直角边,谁是斜边.2ABCabcc4m3mDCBA8m4.8mABCD7cm课堂训练:A组1、求下图中字母所代表的正方形的面积。A=______B=_______2、根据图示条件,求出未知边长度,并写在三角形边上。3、在Rt△ABC中,∠C是直角,已知其中两边,求另一条边。ABACBC草图①43②106③1312B组:1、如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为_______cm2354ABC(图1)86ABC(图2)3aABC(图3)2、美国第二十届总统加菲尔德也曾给出勾股定理的一种证法,如图,他用两个全等的直角三角形和一个等腰直角三角形拼出了一个直角梯形,请你根据此图用拼图法验证勾股定理。C组:1、如图,求等腰三角形ABC的面积。4