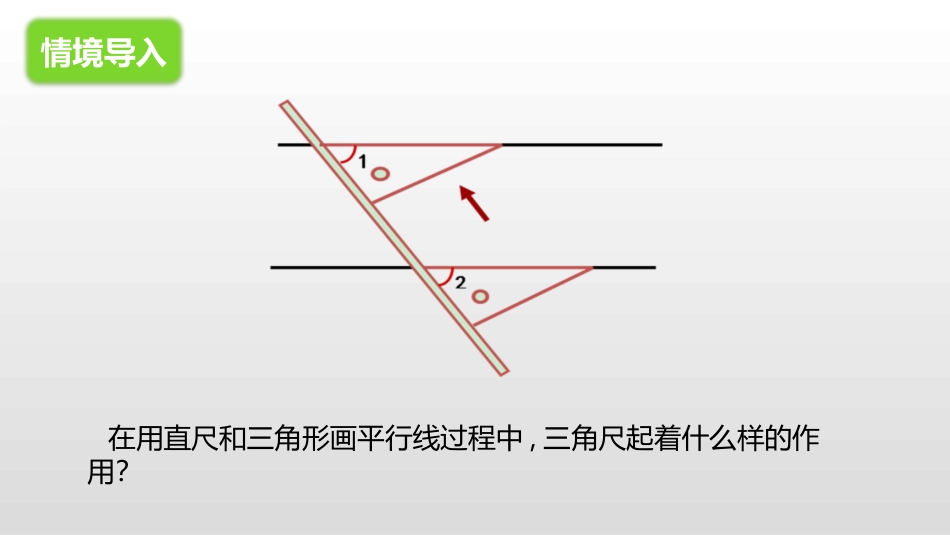
人教五•四学制2011课标版初中数学七年级上册《12.2.2平行线的判定》齐齐哈尔市第七中学校教师:娄晶本节目标123经历探索两直线平行条件的过程,理解两直线平行的条件。掌握平行线的三种判定方法,并初步运用它们进行简单的推理论证。初步学会简单的论证和推理,认识几何证明的必要性和证明过程的严密性。情境导入在用直尺和三角形画平行线过程中,三角尺起着什么样的作用?预习反馈1.如图,∠1=70°,在给出的下列条件中,能判定AB∥CD的条件的是()A.∠2=70°B.∠3=110°C.∠4=70°D.∠5=70°2.如图,∠1=65°,∠B=65°,可以判断____∥____,理由是_________________________.DCBA543213EDCBA1DCBADADBC同位角相等,两直线平行预习反馈3.∠3=30°,当∠ABE=______时,就能使BE∥CD?4.如图所示,如果∠D=∠EFC,那么()A.AD∥BCB.EF∥BCC.AB∥DCD.AD∥EFD150°3EDCBA1DCBAFEDCBAA课堂探究1l2lAB如果∠1=∠2那么l1∥l2思考:三角板可以使哪些角相等?12课堂探究平行线判定方法1两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简单说成:同位角相等,两直线平行几何语言表述:∵∠1=∠2(已知)∴AB∥CD(同位角相等,两直线平行)课堂探究木工师傅使用角尺画平行线,有什么道理?证明:∵∠1=∠2(已知)∠1=∠3(对顶角相等)∴∠2=∠3(等量代换)∴AB∥CD(同位角相等,两直线平行)课堂探究DABE1342如图,直线AB、CD被EF所截,如果∠1=∠2,能得出AB∥CD吗?CDABE1342平行线判定方法2两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.简单说成:内错角相等,两直线平行课堂探究几何语言表述:∵∠1=∠2(已知)∴AB∥CD(内错角相等,两直线平行)CDABE1342如图:如果2+4=180°能判定AB//CD吗?课堂探究证明:∵∠2+∠4=180°(已知)∠3+∠4=180°(邻补角定义)∴∠2=∠3(等角的补角相等)∴AB∥CD(同位角相等,两直线平行)DABE1342课堂探究平行线判定方法3两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.简单说成:同旁内角互补,两直线平行几何语言表述:∵∠2+∠4=180°(已知)∴AB∥CD(同旁内角互补,两直线平行)典例精析abc12例:在同一平面内,两条直线垂直于同一条直线,这两条直线平行吗?为什么?答:垂直于同一条直线的两条直线平行.理由:如图,∵b⊥a,c⊥a(已知)∴∠1=∠2=90°(垂直定义)∴b∥c(同位角相等,两直线平行)随堂检测如图,在下列条件中,能判断AD∥BC的是()A.∠DAC=∠BCAB.∠DCB+∠ABC=180°C.∠ABD=∠BDCD.∠BAC=∠ACDA本课小结同位角相等内错角相等同旁内角互补两直线平行平行线的判定示意图平行线的判定示意图判定数量关系位置关系作业布置家庭作业:完成本节的同步练习预习作业:预习《平行线的性质》导学案中的“预习案”