平行线的判定方法2、3-(2)VIP免费

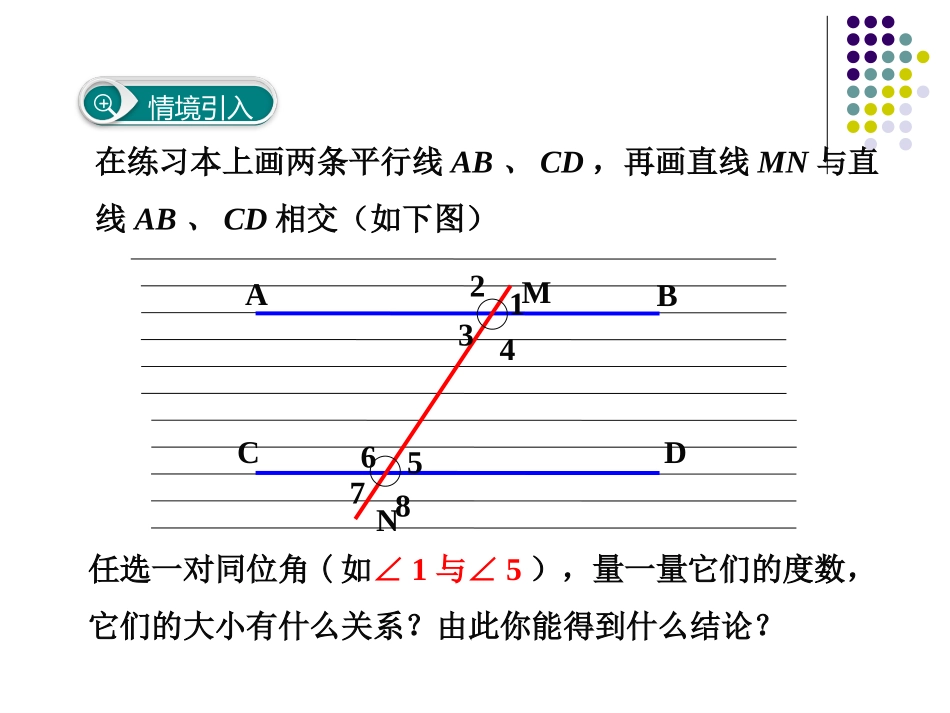
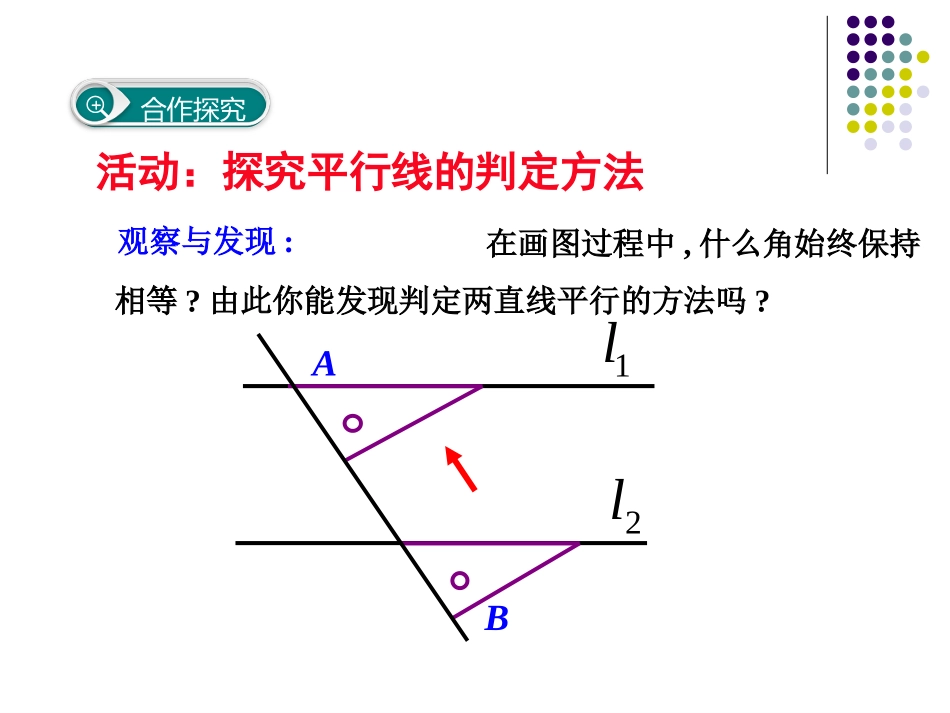
10.2平行线的判定第2课时平行线的判定方法第10章相交线、平行线与平移情境引入ABCDMN在练习本上画两条平行线AB、CD，再画直线MN与直线AB、CD相交（如下图）任选一对同位角(如∠1与∠5），量一量它们的度数，它们的大小有什么关系？由此你能得到什么结论？34152687合作探究观察与发现:1l2l在画图过程中,什么角始终保持相等?由此你能发现判定两直线平行的方法吗?活动：探究平行线的判定方法AB一般地,判断两直线平行有下面的方法:判定方法1两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简单说成：同位角相等,两直线平行.如图：（1）由1=2，可推出a//b吗？为什么？说一说答：可以推出a//b.根据同位角相等，两直线平行.答：可以推出a//b.根据同位角相等，两直线平行.12abc12abc∵∠1=2∠（已知）∴a∥b（同位角相等，两直线平行）书写格式：4123ABCEFD5HG如果,能判定哪两条直线平行?∠1=2∠∠2=5∠∠3=4∠想一想两条直线被第三条直线所截，同时得到同位角、内错角和同旁内角，由同位角相等可以判定两直线平行，那么，能否利用内错角，或同旁内角来判定两直线平行呢？思考：由3=2，可推出a//b吗？如何推出？写出你的推理过程.解：1=3(已知）3=2（对顶角相等）1=2a//b(同位角相等，两直线平行）21cba3说一说数学转化思想判定方法2两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.简单说成：内错角相等,两直线平行.一般地,判断两直线平行有下面的方法:如图，∠1=2∠，且∠1=3∠，AB和CD平行吗？ABCD123想一想如果1+2=1800能判定a//b吗?c解:能,因为1+2=1801+3=180所以2=3所以a//b2ba13说一说数学转化思想判定方法3两条直线被第三条直线所截，如果同旁内角互补，那么这两条直线平行.简单说成：同旁内角互补,两直线平行.一般地,判断两直线平行有下面的方法:如图：B=D=45°，C=135°，问图中有哪些直线平行？答：AB//CD，AD//BC∵B=45°（已知）C=135°（已知）B+C=180°AB//CD（同旁内角互补，两直线平行）同理：AD//BCDCBA想一想判定两条直线平行的方法文字叙述符号语言图形相等两直线平行∵(已知)∴a∥b相等两直线平行互补，两直线平行∵(已知)∴a∥b∵∴a∥b同位角内错角同旁内角∠1=2∠∠3=2∠∠2+4=180°∠abc1234同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行.课堂小结1.如图,不能判定的是（）12//ll（A）∠2＝∠3（B）∠1＝∠4（C）∠1＝∠2（D）∠1＝∠3DD13241l2l随堂训练2.如图,∠1＝∠2,则下列结论正确的是（）A.AD//BCB.AB//CDC.AD//EFD.EF//BCCCABCDEF123.如图，哪些直线平行，哪些直线不平行？1l3l4l2l与平行，与不平行3l4l1l2l60o50o120o60o4.如图，哪些条件能判定直线ABCD∥?1432ADCB5.如图:可以确定AB∥CE的条件是()A.2=∠∠BB.1=∠∠AC.3=∠∠BD.3=∠∠AAEBCD123C6.如图，已知∠1=30°，∠2或∠3满足条件________________________，则a//b.6.如图，已知∠1=30°，∠2或∠3满足条件________________________，则a//b.213abc∠2＝150或∠3＝30°∠2＝150或∠3＝30°7.直线ab被直线c所截，给出下列条件：（1）∠1=2∠；（2）∠3=6∠；（3）∠4=1∠；（4）∠6+7=180°.∠其中能识别a//b的条件序号是.(1)(2)(4)48621537abc