20070919高一数学(131-1函数单调性的概念)VIP免费

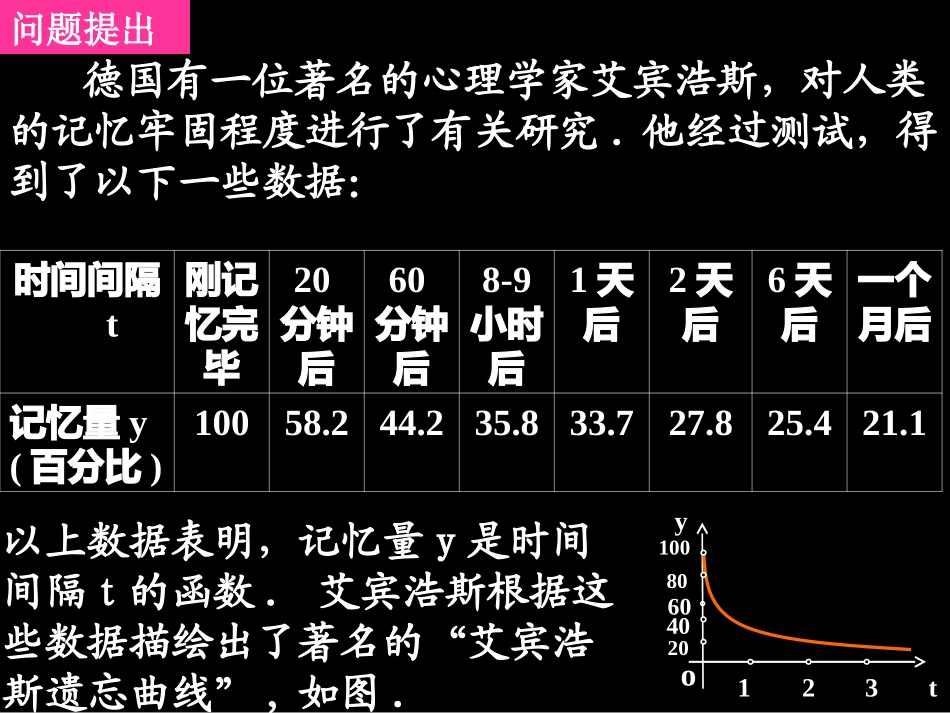
1.3.1单调性与最大（小）值第一课时函数单调性的概念问题提出德国有一位著名的心理学家艾宾浩斯，对人类的记忆牢固程度进行了有关研究.他经过测试，得到了以下一些数据：时间间隔t刚记忆完毕20分钟后60分钟后8-9小时后1天后2天后6天后一个月后记忆量y(百分比)10058.244.235.833.727.825.421.1以上数据表明，记忆量y是时间间隔t的函数.艾宾浩斯根据这些数据描绘出了著名的“艾宾浩斯遗忘曲线”,如图.123tyo20406080100思考1:当时间间隔t逐渐增大你能看出对应的函数值y有什么变化趋势？通过这个试验，你打算以后如何对待刚学过的知识?思考2:“艾宾浩斯遗忘曲线”从左至右是逐渐下降的，对此，我们如何用数学观点进行解释？tyo20406080100123知识探究（一）yxo考察下列两个函数:()fxx2()(0)fxxx（1）；(2)xyo思考1:这两个函数的图象分别是什么？二者有何共同特征？思考2:如果一个函数的图象从左至右逐渐上升，那么当自变量x从小到大依次取值时，函数值y的变化情况如何？()fx12xx1()fx2()fx思考3:如图为函数在定义域I内某个区间D上的图象，对于该区间上任意两个自变量x1和x2，当时，与的大小关系如何？xyox1x2()yfx1()fx2()fx思考4:我们把具有上述特点的函数称为增函数，“那么怎样定义函数在区间D上是增函数”？()fx()fx12,xx1x2x1()fx2()fx)(xf对于函数定义域I内某个区间D上的任意两个自变量的值，若当<时，都有<,则称函数在区间D上是增函数.知识探究（二）考察下列两个函数:()fxx2()(0)fxxx（1）；(2)1()fx2()fx()yfxxyoxoy思考1:这两个函数的图象分别是什么？二者有何共同特征？()fx思考2:我们把具有上述特点的函数称为减函数，那么怎样定“义函数在区间D上是减函数”？2()fxxyox1x2()yfx1()fx()fx12,xx1x2x1()fx2()fx)(xf对于函数定义域I内某个区间D上的任意两个自变量的值，若当<时，都有>,则称函数在区间D上是减函数.()fx12()()fxfx思考3:对于函数定义域I内某个区间D上的任意两个自变量的值，若当时，都有,则函数在区间D上是增函数还是减函数？12,xx12xx2()(1)fxx()fx()fx思考4：如果函数y=f(x)在区间D上是增函数或减函数，则称函数在这一区间具有（严格的）单调性，区间D叫做函数的单调区间.那么二次函数在R上具有单调性吗？函数的单调区间如何？理论迁移-5-3136oxy()yfx()yfx例1如图是定义在闭区间[-5，6]上的函数的图象，根据图象说出的单调区间，以及在每一单调区间上，函数是增函数还是减函数.()yfx说明1.函数的单调区间可以是开的，也可以是闭的，也可以是半开半闭的。只要单调区间端点是定义域内的，该端点处可开可闭，一般写成闭。如果不是定义域内的，就只能写成开的。问：上题中，函数f(x)的减区间为[-5,-2）,[1,3），能不能写成[-5,-2）∪[1,3）？2、一般地，若函数f(x)在区间A、B上是单调增(或减)函数，那么在区间AB∪上不一定是单调增(或减)函数，所以我们在写单调区间时不能用并集符号，只能用逗号或和隔开；而且每个单调区间要写成最大的（完整）。问：若函数地f(x)在区间D上具有单调性，那么函数f(x)在区间D上的子区间上具有相同的单调性吗？3、若函数地f(x)在区间D上具有单调性，那么函数f(x)在区间D上的子区间上具有相同的单调性。例2：证明函数在R上是增函数。xxxf3)(证明：任取2121,,xxRxx且)()()()(23213121xxxxxfxf则)(213231xxxx）（)()(2122212121xxxxxxxx）（)1)((22212121xxxxxx1432)(2222212121xxxxxxx143)2()(2222121xxxxx21xx 021xx0143222221xxx）而（)()(,0)()(2121xfxfxfxf即上是增函数。在Rxxxf3)(【证明】设x1，x2∈[0，＋∞)，且x10.∴f(x1)－f(x2)<0，即f(x1)