26.1.1反比例函数概念VIP免费

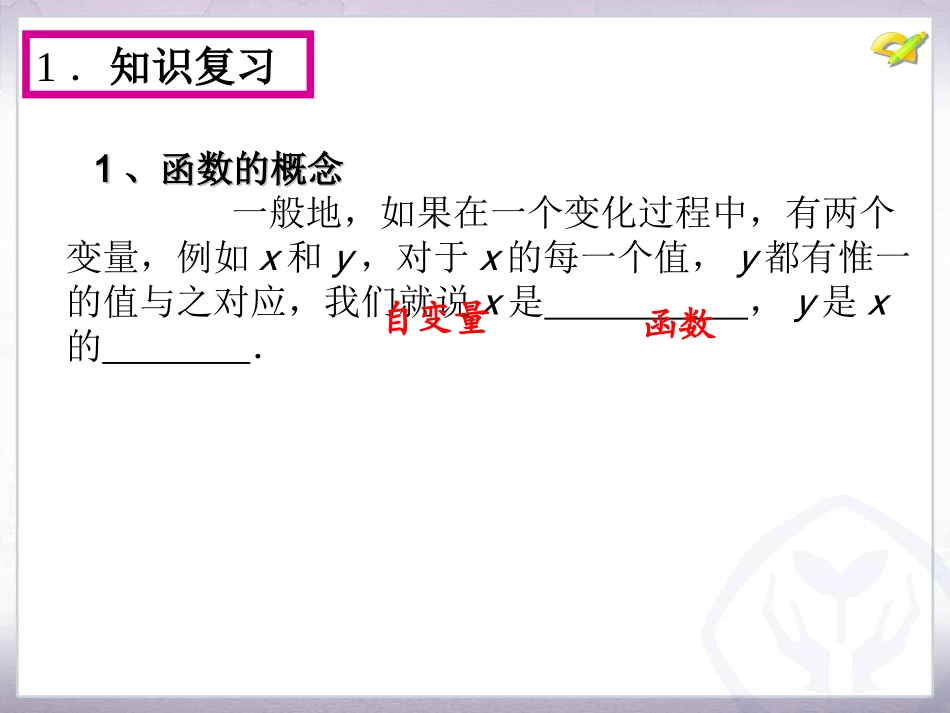
26.1.1反比例函数的概念九年级下册1．知识复习11、函数的概念、函数的概念一般地，如果在一个变化过程中，有两个变量，例如x和y，对于x的每一个值，y都有惟一的值与之对应，我们就说x是，y是x的．自变量函数1．知识复习22、几类学过的函数、几类学过的函数在下列实际问题中,变量间的对应关系可用怎样的函数式表示?对应是哪类函数？（1）一辆以60km/h匀速行驶的汽车，它行驶的距离S(单位：km)随时间t(单位：h)的变化而变化。____________________（2）一辆汽车的油箱中现有汽油50升，如果不再加油，平均每千米耗油量为0.1升，油箱中剩余的油量y(单位：升)随行驶里程x（单位：千米）的变化而变化。_＿＿＿＿_________________（3）正方形的面积S随边长x的变化而变化。_________＿＿＿_________函数关系式为：S=60t函数关系式为：y=50－0.1x函数关系式为：S=x22．知识探究（4）某住宅小区要种植一个面积为1000m2的矩形草坪，草坪的长y（单位：m）随宽x（单位：m）的变化而变化。_____________________（5）已知北京市的总面积为1.68×104平方千米，人均占有的土地面积S（单位：平方千米/人）随全市总人口n（单位：人）的变化而变化。______________________（6）京沪线铁路全程为1463km，某次列车的平均速度v（单位：km/h）随此次列车的全程运行时间t（单位：h）的变化而变化。____________________函数关系式为：xy1000函数关系式为：nS41068.1函数关系式为：tv14632．知识探究tv1463xy1000nS41068.1你能否根据这一类函数的共同特点，写出这种函数的一般形式？xky（k为常数，k≠0）2．知识探究3．知识归纳►知识点一反比例函数的概念反比例函数：一般地，形如__________(k为常数，k≠0)的函数，叫做反比例函数．k叫做比例系数.y＝kx反比例函数的自变量取值范围：___________x≠0反比例函数的变形形式：（1）_____________；（2）_____________xy=k（k≠0）y=k·x-1（k≠0）函数值取值范围：___________y≠0探究问题一识别反比例函数例1下列关系式中，y是x的反比例函数的有________(填写序号)．(1)y＝3x；(2)y＝x2；(3)y＝4x＋5；(4)y＝1x＋2；(5)xy＝2014；(6)yx＝10.[答案](5)4．知识应用5．知识巩固1、下列关系式中的y是x的反比例函数吗？如果是，比例系数k是多少？完成学案练习14．知识应用探究问题二反比例函数概念的考察例2当m为何值时，函数是反比例函数，并求出其函数解析式．21mxmy5．知识巩固2、已知函数是正比例函数，则m=____；函数是反比例函数，则m=_____7mxy73mxy3．知识归纳►知识点二反比例函数解析式的确定由反比例函数的定义知，只要确定_______，就确定了反比例函数的解析式．步骤：(1)先根据题意，设出反比例函数的解析式为_____________________；(2)代入x与y的一组对应值；(3)通过解方程，求出常数___________．y＝kx(k为常数，k≠0)k的值k待定系数待定系数法求解析法求解析式式例3已知y是x的反比例函数，当x=2时，y=6．（1）写出y与x的函数关系式（2）求当x=4时,y的值4．知识应用探究问题三求反比例函数的解析式yy与与xx成反成反比比4．知识应用探究问题二求反比例函数的解析式例4已知y是x的反比例函数，下表给出了x与y的一些值：x－1－12y4－4－2(1)写出这个反比例函数的解析式；(2)根据函数解析式完成上表．5．知识巩固3、已知y与x2成反比例，当x＝3时，y＝4，（1）写出y和x之间的函数解析式;（2）求x＝1.5时y的值.作业与练习1、完成学案P352、书P3练习第1，2，3题3、书P8习题26.1第1，2题