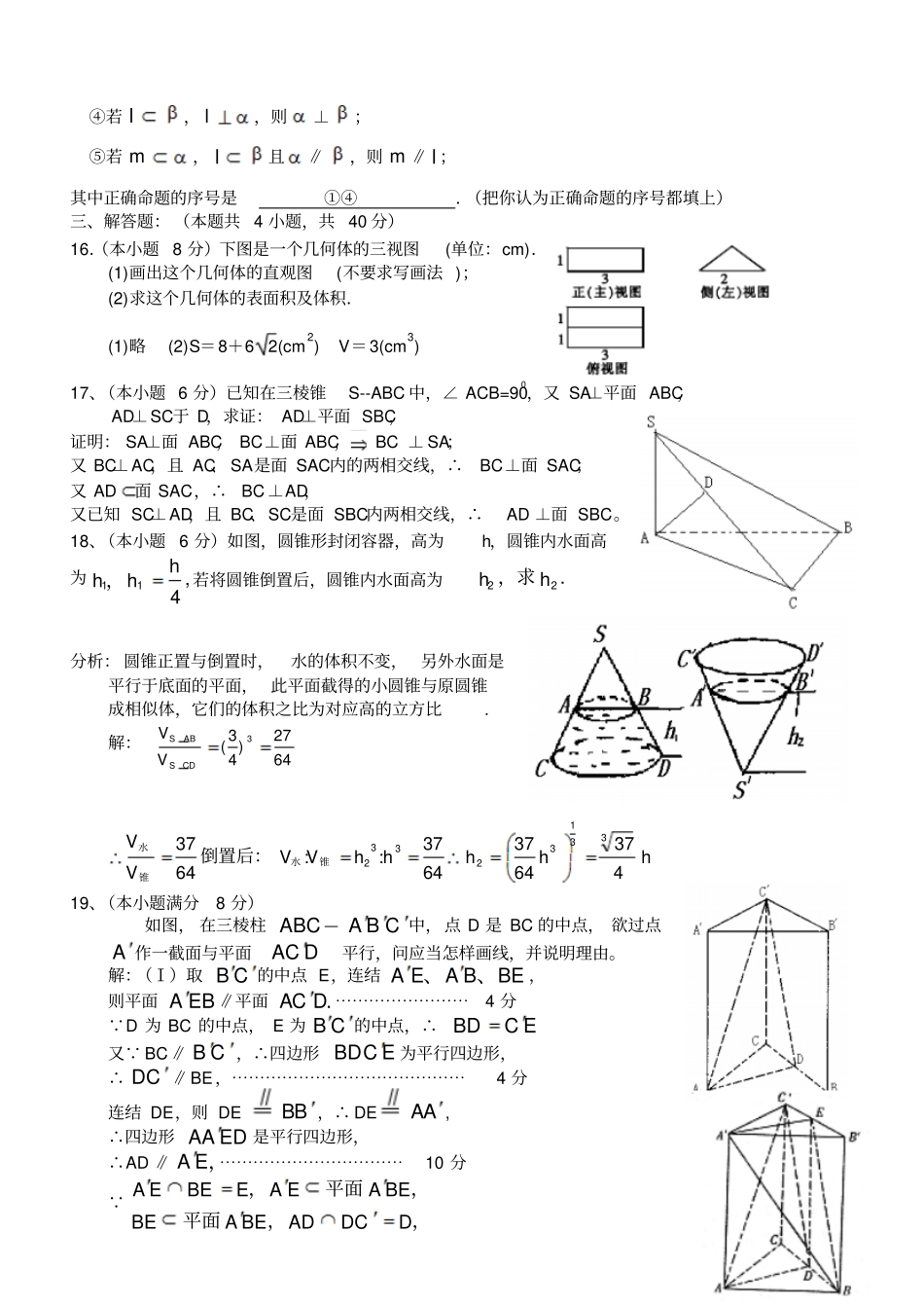
高中数学学习材料(灿若寒星精心整理制作)高中数学必修2立体几何部分测试卷答案班级姓名学号一、选择题:(本大题共8小题,每小题4分,共32分。在每小题给出的四个选项中,只有一项是符合题目要求的)1、垂直于同一条直线的两条直线一定(D)A、平行B、相交C、异面D、以上都有可能2、过直线l外两点作与直线l平行的平面,可以作(D)A.1个B.1个或无数个C.0个或无数个D.0个、1个或无数个3、正三棱锥底面三角形的边长为3,侧棱长为2,则其体积为(C)A.41B.21C.43D.494、右图是一个实物图形,则它的左视图大致为(D)5、已知正四棱台的上、下底面边长分别为3和6,其侧面积等于两底面积之和,则该正四棱台的高是(A)A.2B.25C.3D.276、已知、是平面,m、n是直线,则下列命题不正确...的是(D)A.若//,mnm,则nB.若,mm,则//C.若,//,mmnn,则D.若//,mn,则//mn7、正六棱柱ABCDEF-A1B1C1D1E1F1的侧面是正方形,若底面的边长为a,则该正六棱柱的外接球的表面积是(B)A.4πa2B.5πa2C.8πa2D.10πa28、如下图,在ABC中,2AB,BC=1.5,120ABC,如图所示。若将ABC绕BC旋转一周,则所形成的旋转体的体积是(D)(A)92(B)72(C)52(D)32(第8题图)二、填空题(本大题共8小题,每小题4分,共28分)9、如图是由单位立方体构成的积木垛的三视图,据此三视图可知,构成这堆积木垛的单位正方体共有7块10、给出下列命题①过平面外一点有且仅有一个平面与已知平面垂直②过直线外一点有且仅有一个平面与已知直线平行③过直线外一点有且仅有一条直线与已知直线垂直④过平面外一点有且仅有一条直线与已知平面垂直其中正确命题的个数为112、已知直线m、n及平面,其中m∥n,那么在平面内到两条直线m、n距离相等的点的集合可能是:①一条直线;②一个平面;③一个点;④空集。其中正确的是①②④。13、一个正四棱柱的各个顶点在一个直径为2cm的球面上.如果正四棱柱的底面边长为1cm,那么该棱柱的表面积为224cm2.14、如右图.M是棱长为2cm的正方体ABCD-A1B1C1D1的棱CC1的中点,沿正方体表面从点A到点M的最短路程是13cm.15、已知两条不同直线m、l,两个不同平面、,给出下列命题:①若l垂直于内的两条相交直线,则l⊥;②若l∥,则l平行于内的所有直线;③若m,l且l⊥m,则⊥;④若l,l,则⊥;⑤若m,l且∥,则m∥l;其中正确命题的序号是①④.(把你认为正确命题的序号都填上)三、解答题:(本题共4小题,共40分)16.(本小题8分)下图是一个几何体的三视图(单位:cm).(1)画出这个几何体的直观图(不要求写画法);(2)求这个几何体的表面积及体积.(1)略(2)S=8+62(cm2)V=3(cm3)17、(本小题6分)已知在三棱锥S--ABC中,∠ACB=900,又SA⊥平面ABC,AD⊥SC于D,求证:AD⊥平面SBC,证明:SA⊥面ABC,BC⊥面ABC,BC⊥SA;又BC⊥AC,且AC、SA是面SAC内的两相交线,∴BC⊥面SAC;又AD面SAC,∴BC⊥AD,又已知SC⊥AD,且BC、SC是面SBC内两相交线,∴AD⊥面SBC。18、(本小题6分)如图,圆锥形封闭容器,高为h,圆锥内水面高为,411hhh,若将圆锥倒置后,圆锥内水面高为hh22,求.分析:圆锥正置与倒置时,水的体积不变,另外水面是平行于底面的平面,此平面截得的小圆锥与原圆锥成相似体,它们的体积之比为对应高的立方比.解:6427)43(3CDSABSVVhhhhhVVVV43764376437::643733132332锥水锥水倒置后:19、(本小题满分8分)如图,在三棱柱ABC—CBA中,点D是BC的中点,欲过点A作一截面与平面DCA平行,问应当怎样画线,并说明理由。解:(Ⅰ)取CB的中点E,连结BEBAEA、、,则平面EBA∥平面.DCA⋯⋯⋯⋯⋯⋯⋯⋯4分 D为BC的中点,E为CB的中点,∴ECBD又 BC∥CB,∴四边形ECBD为平行四边形,∴CD∥BE,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4分连结DE,则DEBB,∴DEAA,∴四边形EDAA是平行四边形,∴AD∥,EA⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯10分 AEBEEAEABEBEABEADDCD,平面,平面,,AD平面DCA,DCACD平面,∴平面EBA∥平面DCA。⋯⋯⋯8分20、(本小题12分)已知四棱锥P-ABCD,底面ABCD是60A、边长为a的菱形,又ABCDPD底,且PD=CD,点M、N分别是棱AD、PC的中点.(1)证明:DN//平面PMB;(2)证明:...