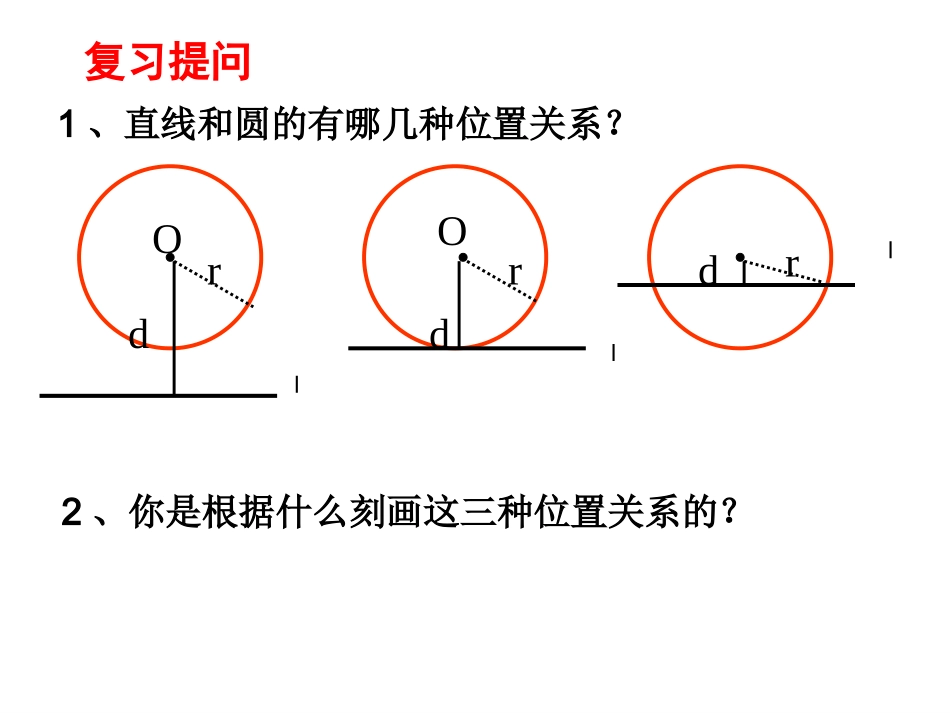
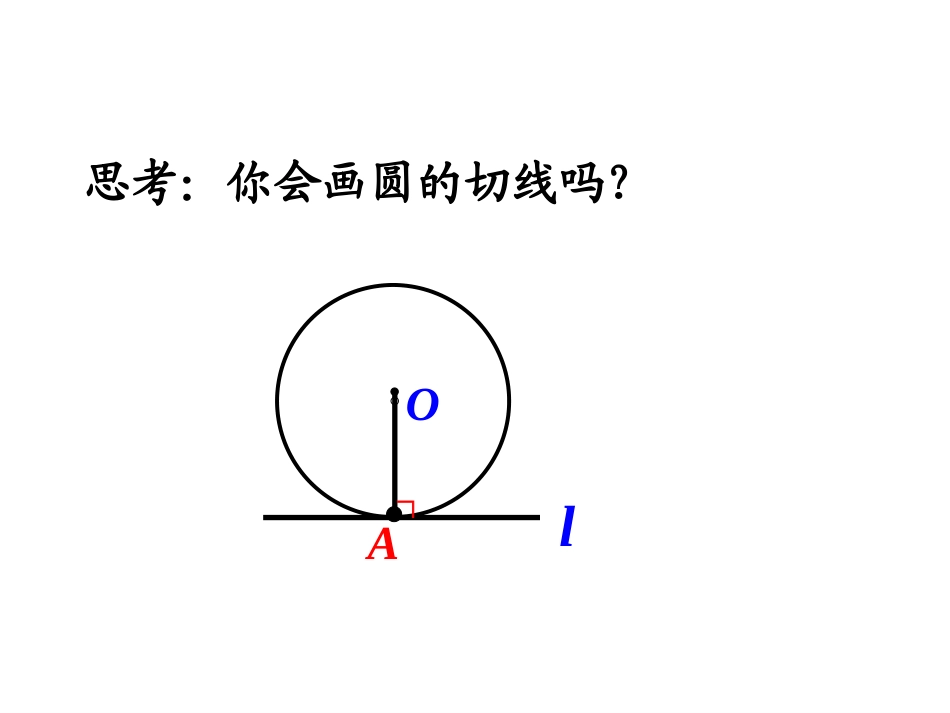
复习提问1、直线和圆的有哪几种位置关系?2、你是根据什么刻画这三种位置关系的?lOOdddrrrll24.2.2直线与圆的位置关系(2)——切线的判定定理●OO思考:你会画圆的切线吗?lA∟lAO∵A点在⊙O上l⊥OA于点A∴直线l是⊙O的切线。∟经过半径的外端并且垂直于这条半径的直线是圆的切线。切线的判定定理:应用格式:归纳1.过半径的外端的直线是圆的切线()2.与半径垂直的直线是圆的切线()3.过半径的端点与半径垂直的直线是圆的切线()××××××精彩源于发现请你总结一下:圆的切线的判定有几种方法?lAO∟切线的判定方法有三种:①直线与圆有唯一公共点;②直线到圆心的距离d等于该圆的半径r;③切线的判定定理.例1、已知如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB。求证:直线AB是⊙O的切线。OBAC1、如图,AB是⊙O的直径,点D在AB的延长线上,AC=CD,点C在⊙O上,∠CAB=30°.求证:DC是⊙O的切线.ABCDO你一定能行例2已知如图,点O为∠BAC角平分线上一点,OD⊥AB于D,以O为圆心,OD为半径作⊙O。求证:⊙O与AC相切。EOABCD2、已知如图,OA=OB=5,AB=8,⊙O的直径为6,求证:AB是⊙O的切线.AOB你一定能行证明:连结OP。∵AB为直径为直径∴OB=OA,BP=PC,∴OP∥AC。又∵PE⊥AC,∴PE⊥OP。∴PE为⊙O的切线。如图如图,△,△ABCABC中,以中,以ABAB为直径的⊙为直径的⊙OO交交边边BCBC于于PP,,BPBP==PCPC,,PEPE⊥⊥ACAC于于EE。。求证求证::PEPE是⊙是⊙OO的切线。的切线。OOAABBCCEEPP超级挑战谈谈今天的收获?1.判定切线的方法有哪些?直线l与圆有唯一公共点到圆心的距离等于圆的半径经过半径外端且垂直这条半径2.证明圆的切线常用辅助线作法:⑴有交点,连半径,证垂直⑵无交点,作垂直,证半径检测题1、切线的判定定理:经过半径的________并且和这条半径______的直线是圆的切线2、如右图,⊙O的直径BC=6,AB=10,则当AC=_____时,AC是⊙O的切线。3、已知如图△ABC内接于⊙O,过点A作直线EF,AB为直径,且∠CAE=∠B,求证:EF是⊙O的切线。●O●P┓11、已知:、已知:PP为⊙为⊙OO外一点,以外一点,以OPOP为直为直径作圆交⊙径作圆交⊙OO于于AA、、BB两点,连接两点,连接PAPA、、PBPB那么那么PAPA、、PBPB是⊙是⊙OO的切线吗?的切线吗?AB你一定能行2、如图,AB是⊙O的直径,点D在AB的延长线上,BD=OB,点C在⊙O上,∠CAB=30°.求证:DC是⊙O的切线.ABCDO你一定能行1、已知如图△ABC内接于⊙O,过点A作直线EF,AB为直径,且∠CAE=∠B,求证:EF是⊙O的切线。FECOBA判断:(1)过半径的外端的直线是圆的切线()(2)与半径垂直的的直线是圆的切线()(3)过半径的端点与半径垂直的直线是圆的切线()××××××OOrrllAAOOrrllAAOOrrllAA2、如图,△ABC中,AB=AC,AO⊥BC于O,OE⊥AC于E,以O为圆心,OE为半径作⊙O.求证:AB是⊙O的切线.FECOBA你一定能行探究1、画与半径OA垂直的直线,当垂足在什么位置时,直线为⊙O的切线?为什么?AO垂足在圆上∟∟∟探究2、过半径的外端点A的直线与OA成什么角时,直线与⊙O相切?为什么?AO∟3、一条直线满足什么位置条件,就能成为⊙O的切线?由此你能得到什么结论?AOAO下图中的直线ll是否为⊙O的切线?为什么?OOllAAOOllAA4.过直径的端点与直径垂直的直线是圆的切线()√OOrrllAAll1、练习(1)已知⊙O半径为3,点O到直线l的距离为5,则l与⊙O有__个交点,位置关系是____。0复习提问相离1、练习(2)已知⊙O半径为3,点O到直线l的距离为3,则l与⊙O有__个交点,位置关系是____。1复习提问相切1、练习(3)已知⊙O半径为3,点O到直线l的距离为2,则l与⊙O有__个交点,位置关系是____。2复习提问相交