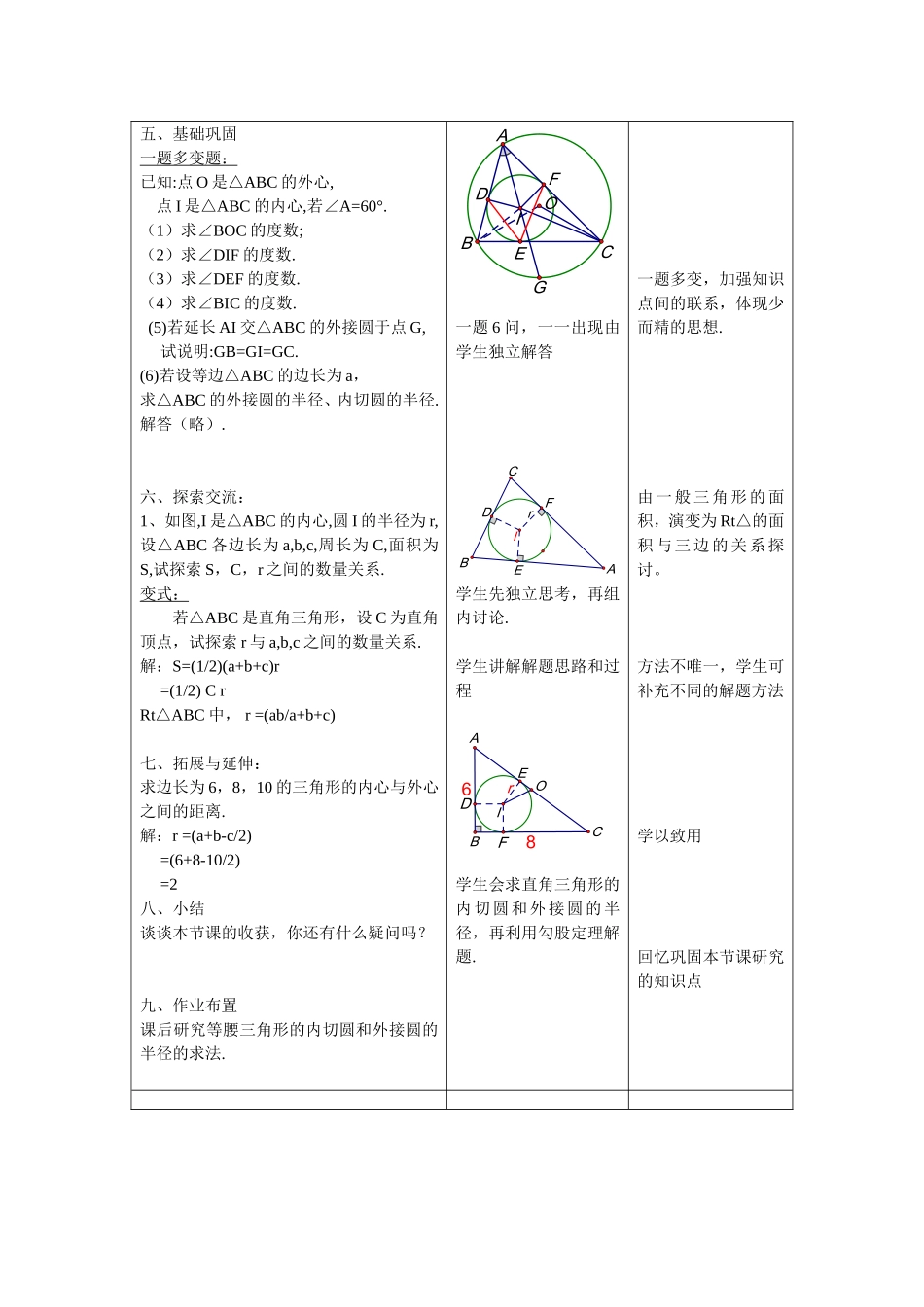
课题:专题研究——三角形的“心”——三角形的外心和内心执教者:杨秀琴教学目标:由三角形的外心和内心的定义,进一步研究三角形外心和内心的性质,以及特殊三角形的内切圆和外接圆的半径的求法探究.教学重点、难点:特殊三角形如:等边三角形、直角三角形的内切圆、外接圆的半径的探讨;对于等腰三角形的外心和内心的一些结论探究.教学过程:教师活动学生活动设计意图一、复习导入:回忆所学过的三角形的“心”,有垂心、重心、外心、内心、旁心等五心,本节课只研究外心和内心。二、自主学习:温故知新(可阅读书本P125和P132)1、什么叫三角形的外心?2、什么叫三角形的内心?3、由三角形的外心和内心性质,能得到更多的结论吗?可添加适当的线和字母。三、交流反馈:1、三角形外心是三角形外接圆的圆心;也是三边中垂线的交点.2、三角形的内心是三角形内切圆的圆心;也是三角平分线的交点.3、小组活动,组内先各抒己见,再汇总三角形外心和内心的性质.四、白板展示:小组讨论:由三角形的外心和内心性质,能得到更多的结论吗?可添加适当的线和字母任务要求:1、第2、4、6、8小组探究三角形的外心.第1、3、5、7、9小组探究三角形的内心.2、白板展示本小组的结论(写序号)3、老师点评一块较清爽的白板,其他小组的白板内容,请小组代表发言补充,还有不同的结论.OABCCBAIDEF学生组内分享预习的成果(各抒己见)小组白板展示组内讨论的结果老师点评一个小组,其余小组补充结论.了解三角形更多的心学生独立自主学习5分钟有关外心和内心的性质。(发散性思维)集思广益(集体的力量是无穷的)任务新生成(答案是发散的)锻炼学生的注意力和表达能力.五、基础巩固一题多变题:已知:点O是△ABC的外心,点I是△ABC的内心,若∠A=60°.(1)求∠BOC的度数;(2)求∠DIF的度数.(3)求∠DEF的度数.(4)求∠BIC的度数.(5)若延长AI交△ABC的外接圆于点G,试说明:GB=GI=GC.(6)若设等边△ABC的边长为a,求△ABC的外接圆的半径、内切圆的半径.解答(略).六、探索交流:1、如图,I是△ABC的内心,圆I的半径为r,设△ABC各边长为a,b,c,周长为C,面积为S,试探索S,C,r之间的数量关系.变式:若△ABC是直角三角形,设C为直角顶点,试探索r与a,b,c之间的数量关系.解:S=(1/2)(a+b+c)r=(1/2)CrRt△ABC中,r=(ab/a+b+c)七、拓展与延伸:求边长为6,8,10的三角形的内心与外心之间的距离.解:r=(a+b-c/2)=(6+8-10/2)=2八、小结谈谈本节课的收获,你还有什么疑问吗?九、作业布置课后研究等腰三角形的内切圆和外接圆的半径的求法.EGFDIOABC一题6问,一一出现由学生独立解答rABCIDEF学生先独立思考,再组内讨论.学生讲解解题思路和过程68rFDEIOABC学生会求直角三角形的内切圆和外接圆的半径,再利用勾股定理解题.一题多变,加强知识点间的联系,体现少而精的思想.由一般三角形的面积,演变为Rt△的面积与三边的关系探讨。方法不唯一,学生可补充不同的解题方法学以致用回忆巩固本节课研究的知识点