第2章解三角形章高效整合VIP免费

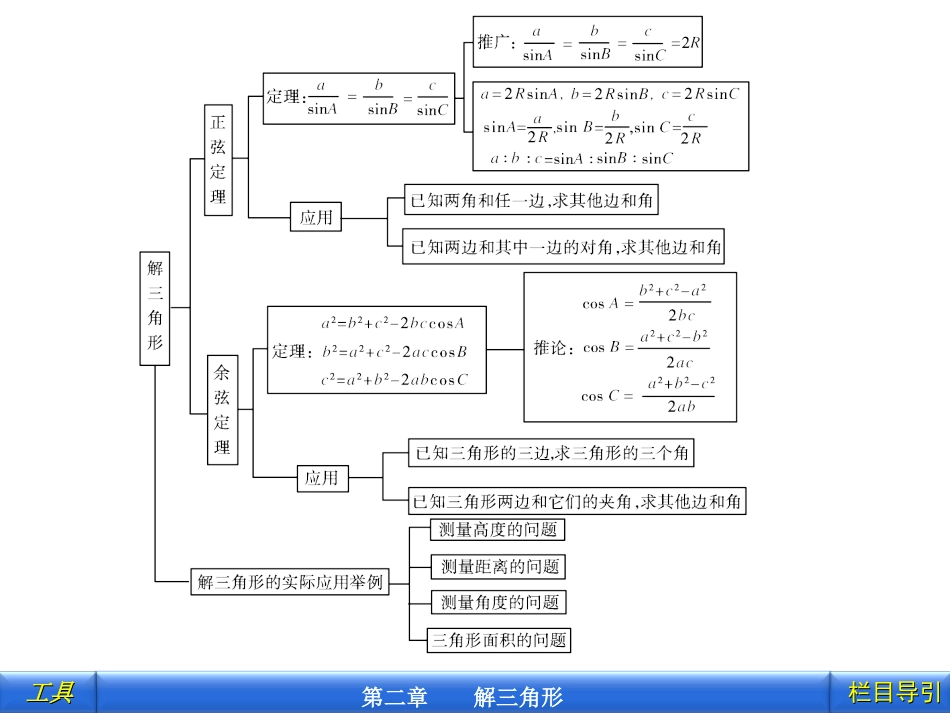
工具工具第二章解三角形栏目导引栏目导引工具工具第二章解三角形栏目导引栏目导引工具工具第二章解三角形栏目导引栏目导引工具工具第二章解三角形栏目导引栏目导引工具工具第二章解三角形栏目导引栏目导引1．掌握正弦定理、余弦定理，并能解决一些简单的三角形度量问题．2．能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题．工具工具第二章解三角形栏目导引栏目导引1．解三角形问题主要有两种题型，一是与三角函数结合起来考查，通过三角变换化简，然后运用正余弦定理求值；二是与平面向量结合，判定三角形形状或结合正余弦定理求值．试题一般是中低档试题，客观题解答题均有可能出现．2．除牢固掌握正余弦定理外，三角形的有关知识如：重心、内心、外心、垂心、内角和、三边关系、面积公式S＝12absinC＝12bcsinA＝12acsinB等也要牢固掌握．工具工具第二章解三角形栏目导引栏目导引工具工具第二章解三角形栏目导引栏目导引解三角形就是已知三角形中的三个独立元素求出其他元素的过程．三角形中的元素有基本元素(边和角)和非基本元素(中线、高、角平分线、外接圆半径和内切圆半径)，解三角形通常是指求未知的元素，有时也求三角形的面积．工具工具第二章解三角形栏目导引栏目导引解斜三角形共包括四种类型：(1)已知三角形的两角和一边；(2)已知两边及夹角；(3)已知三边；(4)已知两边和一边的对角．其中类型(4)中应特别注意解的情况．工具工具第二章解三角形栏目导引栏目导引在△ABC中，(1)已知a＝3，b＝2，B＝45°，求A、C、c；(2)已知sinA∶sinB∶sinC＝(3＋1)∶(3－1)∶10，求最大角．解析：(1)由正弦定理及已知条件有3sinA＝2sin45°，得sinA＝32， a＞b，∴A＞B＝45°，工具工具第二章解三角形栏目导引栏目导引∴A＝60°或120°.当A＝60°时，C＝180°－45°－60°＝75°，c＝bsinCsinB＝2sin75°sin45°＝6＋22，当A＝120°时，C＝180°－45°－120°＝15°，c＝bsinCsinB＝2sin15°sin45°＝6－22.工具工具第二章解三角形栏目导引栏目导引(2)根据正弦定理可知a∶b∶c＝sinA∶sinB∶sinC＝(3＋1)∶(3－1)∶10，∴边c最大，即角C最大．设a＝(3＋1)k，b＝(3－1)k，c＝10k，则cosC＝a2＋b2－c22ab＝3＋12＋3－12－10223＋13－1＝－12. C∈(0，π)，∴C＝2π3.工具工具第二章解三角形栏目导引栏目导引在△ABC中，a、b、c分别是∠A、∠B、∠C的对边长．已知b2＝ac且a2－c2＝ac－bc.(1)求∠A的大小；(2)求bsinBc的值．解析：(1) b2＝ac且a2－c2＝ac－bc，∴a2－c2＝b2－bc，∴b2＋c2－a2＝bc，∴cosA＝b2＋c2－a22bc＝bc2bc＝12，∴A＝60°.工具工具第二章解三角形栏目导引栏目导引(2)方法一：在△ABC中，由正弦定理得：sinB＝bsinAa， b2＝ac，∴ba＝cb.∴sinB＝bsinAa＝c·sinAb，∴bsinBc＝sinA＝sin60°＝32.工具工具第二章解三角形栏目导引栏目导引方法二：在△ABC中，由面积公式得：12bcsinA＝12acsinB b2＝ac，∴bcsinA＝b2sinB，∴bsinBc＝sinA＝sin60°＝32.工具工具第二章解三角形栏目导引栏目导引判断三角形的形状，一般有以下两种途径：将已知条件统一化成边的关系，用代数方法求解；将已知条件统一化成角的关系，用三角知识求解，在解三角形时常用的结论有：1．在△ABC中，A＞B⇔a＞b⇔sinA＞sinB⇔cosA＜cosB.2．在△ABC中，a2＋b2＜c2⇔π2＜C＜π，a2＋b2＝c2⇔cosC＝0⇔C＝π2，a2＋b2＞c2⇔cosC＞0⇔0