6.1平方根(1)(新人教版)VIP免费

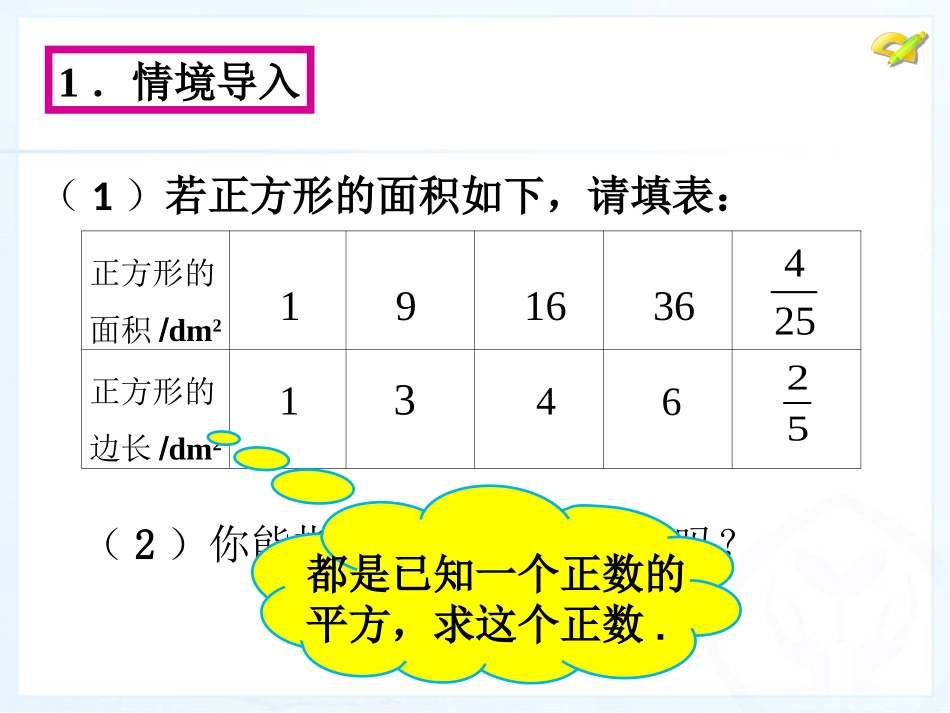
6.1平方根（第三课时）复习回顾（1）什么是算数平方根？怎样表示？（2）256的算术平方根是_____;5的算术平方根是________;(3)下列各式有意义的条件是什么？（4）一块正方形菜地的边长是3米，这块菜地的面积是多少平方米？已知一块正方形菜地的面积是9平方米，求它的边长；如果一个数的平方等于9，这个数是多少？.21,3xx（1）若正方形的面积如下，请填表：（2）你能指出它们的共同特点吗？正方形的面积/dm2191636正方形的边长/dm24251346251．情境导入都是已知一个正数的平方，求这个正数.例如，由于,5是25的算术平方根，即．规定：0的算术平方根是0，也就是说，若，则．一般地，如果一个正数的平方等于，即，那么这个正数叫做的算术平方根．的算术平方根记为，读作“根号”,叫做被开方数．2(0)xaxxa2xaxaaaaaa25252552．总结概念例1求下列各数的算术平方根：（1）；（2）；（3）．解：（1）因为，所以100的算术平方根是10．即．10049640.0001210100100=103．例题解析解：（2）因为，所以的算术平方根是．即．3．例题解析2749864496478497648例1求下列各数的算术平方根：（1）；（2）；（3）．10049640.0001解：（3）因为，所以0.0001的算术平方根是0.01．即．3．例题解析20.010.00010.00010.01例1求下列各数的算术平方根：（1）；（2）；（3）．10049640.0001求下列各式的值：（1）；（2）；（3）；（4）．解：（1）；（2）；（3）；（4）．19252401193255244004．练习5．提出问题被开方数的大小与对应的算术平方根的大小之间有什么关系呢？-4有算术平方根吗？什么数才有算术平方根？例2下列各式是否有意义，为什么？（1）；（2）；（3）；（4）．44232110解：（1）无意义；（4）有意义．（3）有意义；（2）有意义；6．例题解析能否用两个面积为1的小正方形拼成一个面积为2的大正方形？6．提出问题6．提出问题能否用两个面积为1dm2的小正方形拼成一个面积为2dm2的大正方形？6．提出问题能否用两个面积为1dm2的小正方形拼成一个面积为2dm2的大正方形？拼成的这个面积为2dm2的大正方形的边长应该是多少呢？6．提出问题?解:设大正方形的边长为xdm，则由算术平方根的定义，得．所以大正方形的边长为dm．22x2x有多大呢？22（1）什么是算术平方根？如何求一个正数的算术平方根？（2）什么数才有算术平方根？7．归纳小结教科书41页练习第1、2题8．布置作业