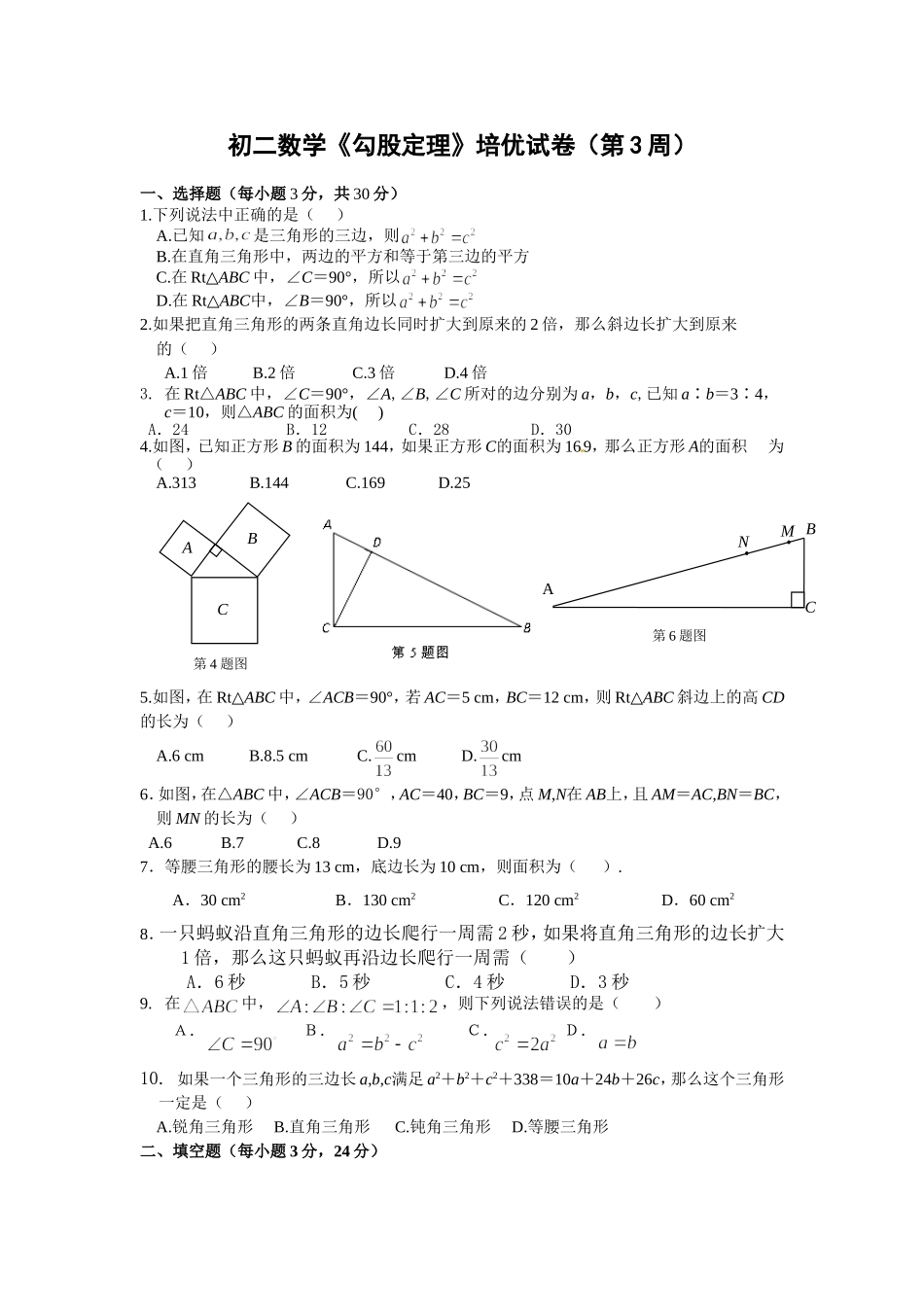
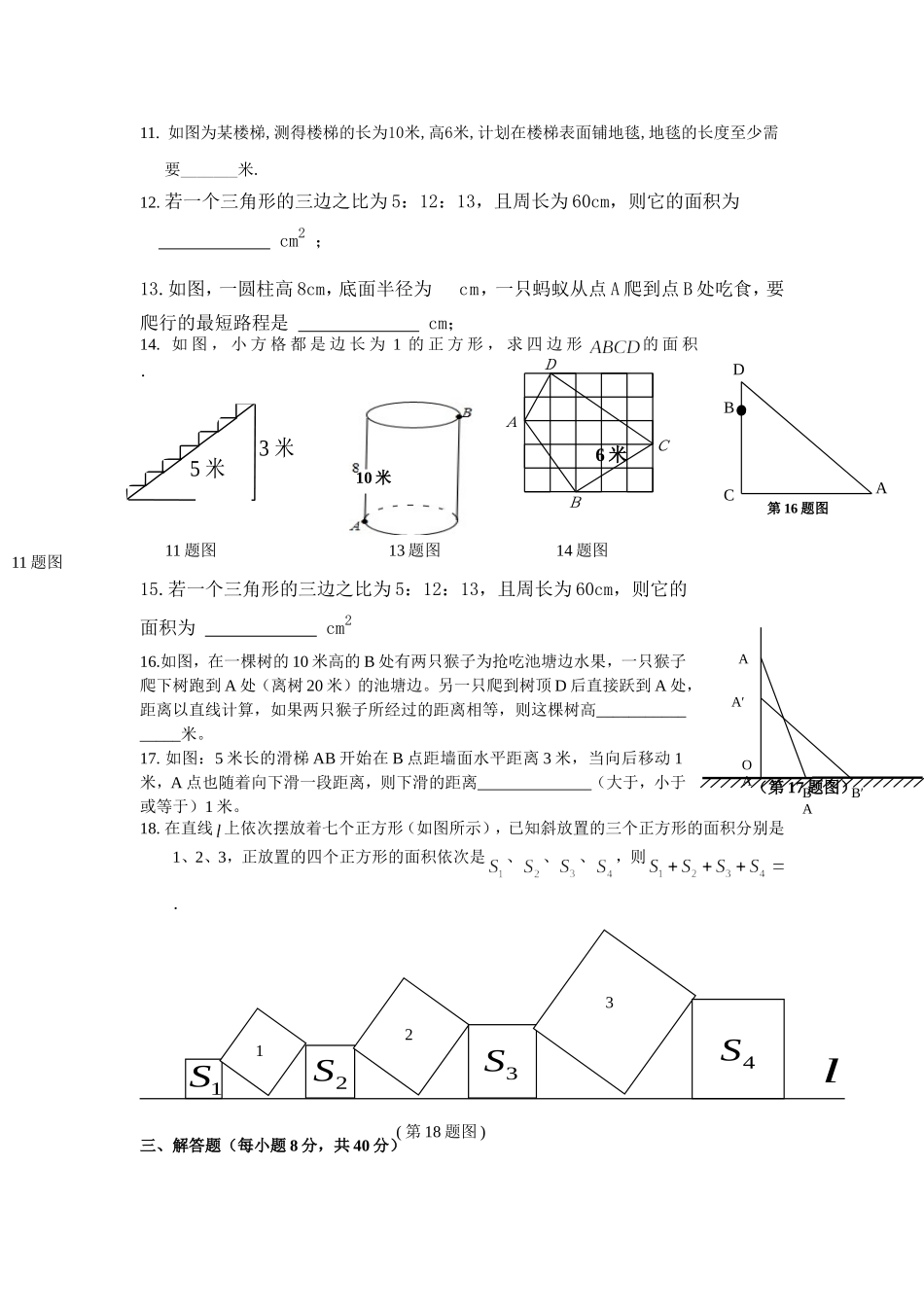
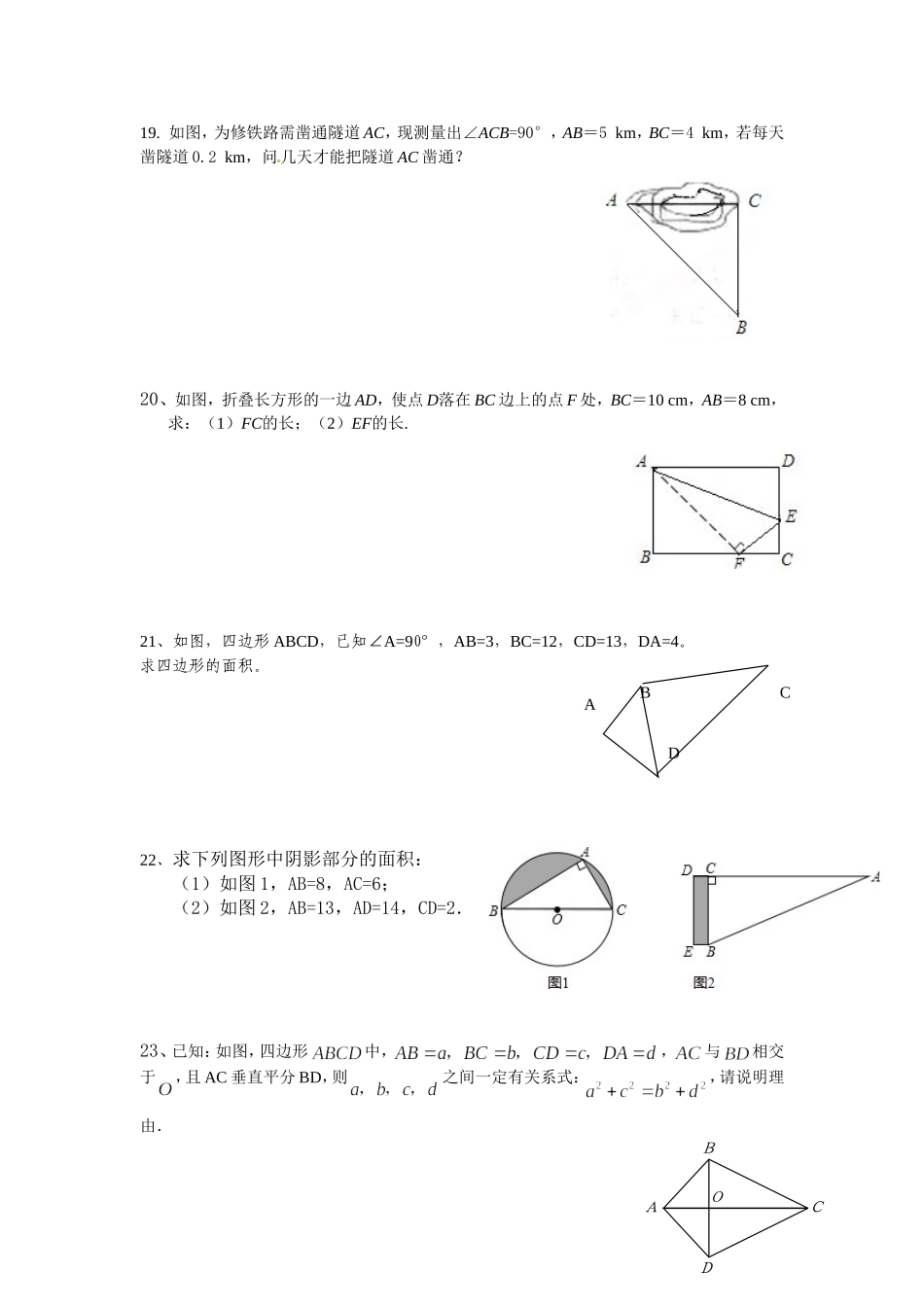
初二数学《勾股定理》培优试卷(第3周)一、选择题(每小题3分,共30分)1.下列说法中正确的是()A.已知是三角形的三边,则B.在直角三角形中,两边的平方和等于第三边的平方C.在Rt△ABC中,∠C=90°,所以D.在Rt△ABC中,∠B=90°,所以2.如果把直角三角形的两条直角边长同时扩大到原来的2倍,那么斜边长扩大到原来的()A.1倍B.2倍C.3倍D.4倍3.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,已知a∶b=3∶4,c=10,则△ABC的面积为()A.24B.12C.28D.304.如图,已知正方形B的面积为144,如果正方形C的面积为169,那么正方形A的面积为()A.313B.144C.169D.255.如图,在Rt△ABC中,∠ACB=90°,若AC=5cm,BC=12cm,则Rt△ABC斜边上的高CD的长为()A.6cmB.8.5cmC.cmD.cm6.如图,在△ABC中,∠ACB=90°,AC=40,BC=9,点M,N在AB上,且AM=AC,BN=BC,则MN的长为()A.6B.7C.8D.97.等腰三角形的腰长为13cm,底边长为10cm,则面积为().A.30cm2B.130cm2C.120cm2D.60cm28.一只蚂蚁沿直角三角形的边长爬行一周需2秒,如果将直角三角形的边长扩大1倍,那么这只蚂蚁再沿边长爬行一周需()A.6秒B.5秒C.4秒D.3秒9.在中,,则下列说法错误的是()A.B.C.D.10.如果一个三角形的三边长a,b,c满足a2+b2+c2+338=10a+24b+26c,那么这个三角形一定是()A.锐角三角形B.直角三角形C.钝角三角形D.等腰三角形二、填空题(每小题3分,24分)ABC第4题图MBCN第6题图A5米3米DBCA第16题图11.如图为某楼梯,测得楼梯的长为10米,高6米,计划在楼梯表面铺地毯,地毯的长度至少需要_______米.12.若一个三角形的三边之比为5:12:13,且周长为60cm,则它的面积为cm2;13.如图,一圆柱高8cm,底面半径为cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是cm;14.如图,小方格都是边长为1的正方形,求四边形的面积.15.若一个三角形的三边之比为5:12:13,且周长为60cm,则它的面积为cm216.如图,在一棵树的10米高的B处有两只猴子为抢吃池塘边水果,一只猴子爬下树跑到A处(离树20米)的池塘边。另一只爬到树顶D后直接跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,则这棵树高________________米。17.如图:5米长的滑梯AB开始在B点距墙面水平距离3米,当向后移动1米,A点也随着向下滑一段距离,则下滑的距离(大于,小于或等于)1米。18.在直线上依次摆放着七个正方形(如图所示),已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是、、、,则.三、解答题(每小题8分,共40分)6米ADCB11题图13题图14题图AA′BAB′OA1S123l2S3S4S(第18题图)(第17题图)10米11题图19.如图,为修铁路需凿通隧道AC,现测量出∠ACB=90°,AB=5km,BC=4km,若每天凿隧道0.2km,问几天才能把隧道AC凿通?20、如图,折叠长方形的一边AD,使点D落在BC边上的点F处,BC=10cm,AB=8cm,求:(1)FC的长;(2)EF的长.21、如图,四边形ABCD,已知∠A=90°,AB=3,BC=12,CD=13,DA=4。求四边形的面积。22、求下列图形中阴影部分的面积:(1)如图1,AB=8,AC=6;(2)如图2,AB=13,AD=14,CD=2.23、已知:如图,四边形中,,与相交于,且AC垂直平分BD,则之间一定有关系式:,请说明理由.ABCDACDOB24、以下是意大利著名画家达·芬奇证明勾股定理的证法:步骤:(1)在一张长方形的纸板上画两个边长分别为a,b的正方形,并连接BC,FE.(2)沿ABCDEF剪下,得两个大小相同的纸板Ⅰ、Ⅱ.请动手做一做.(3)将纸板Ⅱ翻转后与Ⅰ拼成其他的图形.(4)比较两个多边形ABCDEF和A’B’C’D’E’F’的面积,你能验证勾股定理吗?