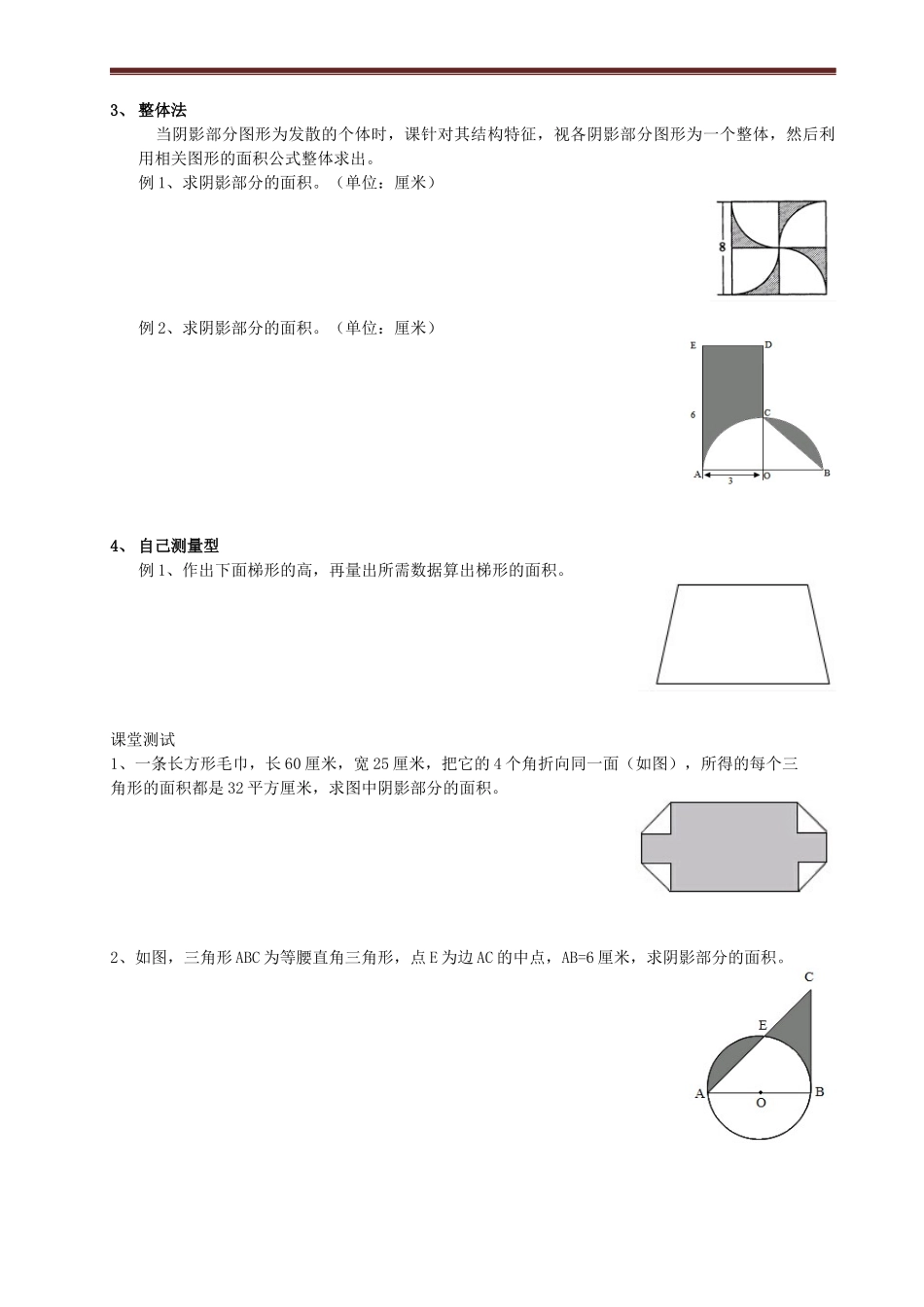
二○一五年小升初专题复习(二)图形面积1、直接法当已知图形为我们熟知的基本图形时,直接代入公式进行计算。(例1图)(例1发散)(例2图)(例3图)例1、下图是平行四边形,面积是36平方米,求阴影部分面积。(单位:米)(如果直角交点为中点,你能快速求面积吗?理由是)例1发散、如图,长方形ABCD的面积为36平方厘米,E、F、G分别为边AB、BC、CD的中点,H为AD边上任意一点,问阴影部分的面积是多少?例2、李大伯用篱笆围一块菜地(其中一面是墙),如图所示。若篱笆全长42米,这块地的面积是多少平方米?例3、如图,正方形的面积是6平方厘米,这个圆的面积是多少平方厘米?2、割补法既是把阴影部分的图形通过割补,拼成规则图形,然后再求面积。(例1图)(例2图)(例3图)例1、如图,正方形变长为2,求图中阴影部分面积。例2、计算阴影部分的面积。例3、观察下图,想一想阴影部分的面积怎样计算简便,请说明理由,并计算阴影部分面积。3、整体法当阴影部分图形为发散的个体时,课针对其结构特征,视各阴影部分图形为一个整体,然后利用相关图形的面积公式整体求出。例1、求阴影部分的面积。(单位:厘米)例2、求阴影部分的面积。(单位:厘米)4、自己测量型例1、作出下面梯形的高,再量出所需数据算出梯形的面积。课堂测试1、一条长方形毛巾,长60厘米,宽25厘米,把它的4个角折向同一面(如图),所得的每个三角形的面积都是32平方厘米,求图中阴影部分的面积。2、如图,三角形ABC为等腰直角三角形,点E为边AC的中点,AB=6厘米,求阴影部分的面积。