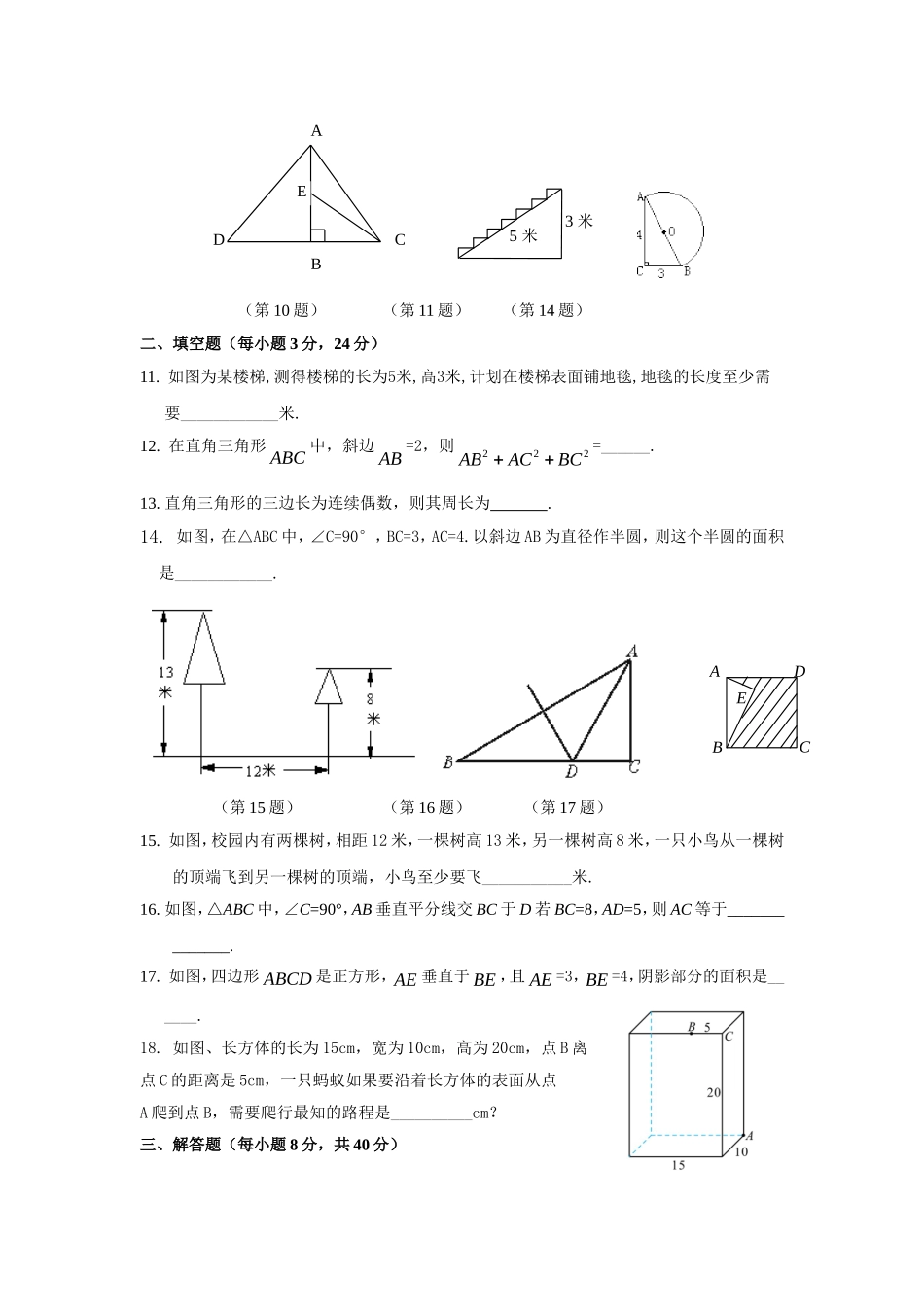
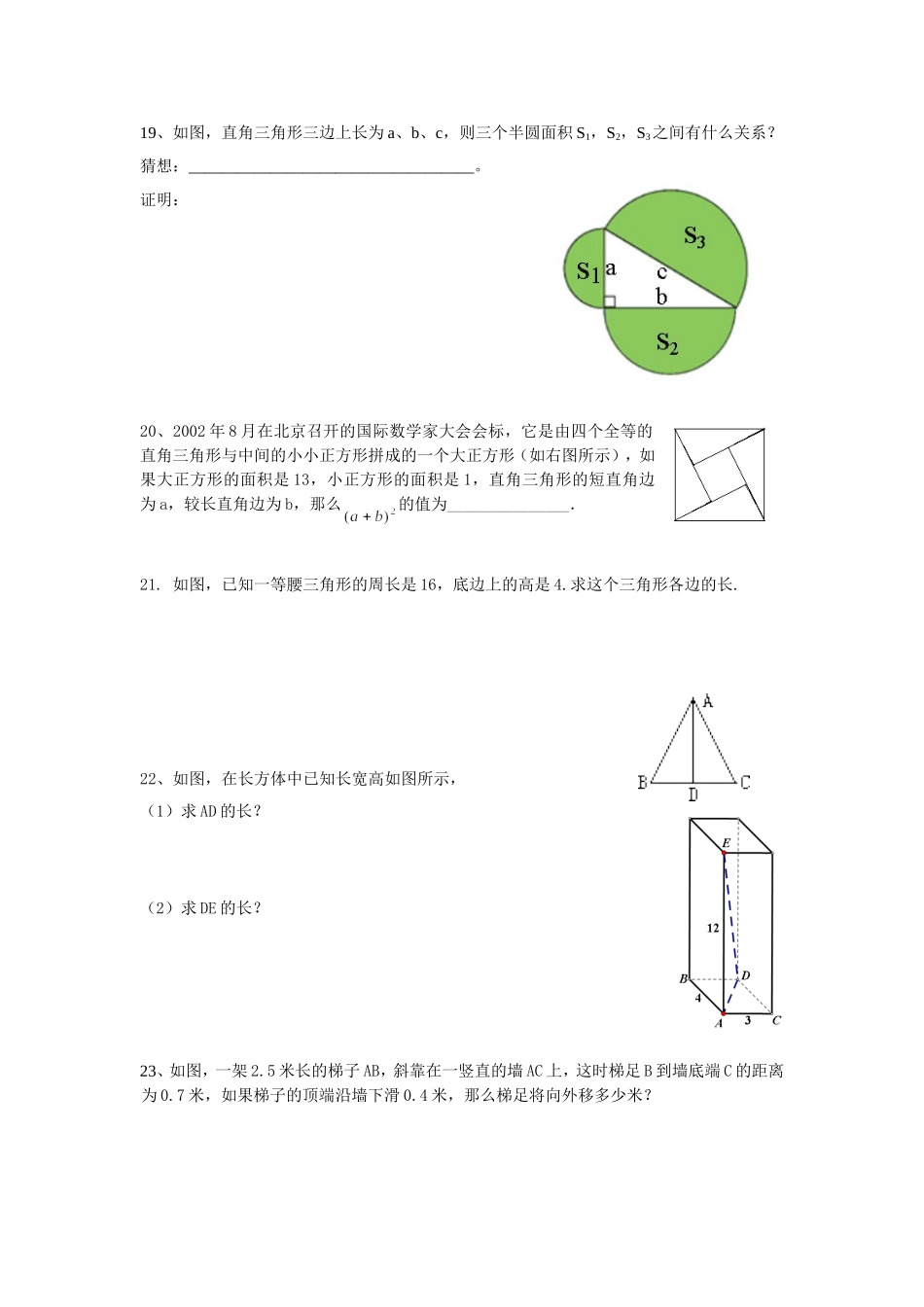
DCBA初二数学《勾股定理》培优试卷(第2周)一、选择题(每小题3分,共30分)1.直角三角形一直角边长为12,另两条边长均为自然数,则其周长为().(A)30(B)28(C)56(D)不能确定2.直角三角形的斜边比一直角边长2cm,另一直角边长为6cm,则它的斜边长(A)4cm(B)8cm(C)10cm(D)12cm3.已知一个Rt△的两边长分别为3和4,则第三边长的平方是()(A)25(B)14(C)7(D)7或254.等腰三角形的腰长为10,底长为12,则其底边上的高为()(A)13(B)8(C)25(D)645.五根小木棒,其长度分别为7,15,20,24,25,现将他们摆成两个直角三角形,其中正确的是()715242520715202425157252024257202415(A)(B)(C)(D)6.将直角三角形的三条边长同时扩大同一倍数,得到的三角形是()(A)钝角三角形(B)锐角三角形(C)直角三角形(D)等腰三角形.7.如图小方格都是边长为1的正方形,则四边形ABCD的面积是()(A)25(B)12.5(C)9(D)8.58.三角形的三边长为abcba2)(22,则这个三角形是()(A)等边三角形(B)钝角三角形(C)直角三角形(D)锐角三角形.9.△ABC是某市在拆除违章建筑后的一块三角形空地.已知∠C=90°,AC=30米,AB=50米,如果要在这块空地上种植草皮,按每平方米草皮a元计算,那么共需要资金().(A)50a元(B)600a元(C)1200a元(D)1500a元10.如图,AB⊥CD于B,△ABD和△BCE都是等腰直角三角形,如果CD=17,BE=5,那么AC的长为().(A)12(B)7(C)5(D)135米3米(第10题)(第11题)(第14题)二、填空题(每小题3分,24分)11.如图为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要____________米.12.在直角三角形ABC中,斜边AB=2,则222ABACBC=______.13.直角三角形的三边长为连续偶数,则其周长为.14.如图,在△ABC中,∠C=90°,BC=3,AC=4.以斜边AB为直径作半圆,则这个半圆的面积是____________.(第15题)(第16题)(第17题)15.如图,校园内有两棵树,相距12米,一棵树高13米,另一棵树高8米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞___________米.16.如图,△ABC中,∠C=90°,AB垂直平分线交BC于D若BC=8,AD=5,则AC等于______________.17.如图,四边形ABCD是正方形,AE垂直于BE,且AE=3,BE=4,阴影部分的面积是______.18.如图、长方体的长为15cm,宽为10cm,高为20cm,点B离点C的距离是5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行最知的路程是__________cm?三、解答题(每小题8分,共40分)EABCDABDCE19、如图,直角三角形三边上长为a、b、c,则三个半圆面积S1,S2,S3之间有什么关系?猜想:___________________________________。证明:20、2002年8月在北京召开的国际数学家大会会标,它是由四个全等的直角三角形与中间的小小正方形拼成的一个大正方形(如右图所示),如果大正方形的面积是13,小正方形的面积是1,直角三角形的短直角边为a,较长直角边为b,那么的值为_______________.21.如图,已知一等腰三角形的周长是16,底边上的高是4.求这个三角形各边的长.22、如图,在长方体中已知长宽高如图所示,(1)求AD的长?(2)求DE的长?23、如图,一架2.5米长的梯子AB,斜靠在一竖直的墙AC上,这时梯足B到墙底端C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么梯足将向外移多少米?CA1B1AB24、大家知道(3、4、5)(5、12、13)(8、15、17)都是勾股数,有人说它们中好像一定有一个是偶数,你认为这种观点正确吗?说明你的理由。25、△ABC中,BCa,ACb,ABc,若∠C=90°,如图(1),根据勾股定理,则222cba,若△ABC不是直角三角形,如图(2)和图(3),请你类比勾股定理,试猜想22ba与2c的关系,并证明你的结论.