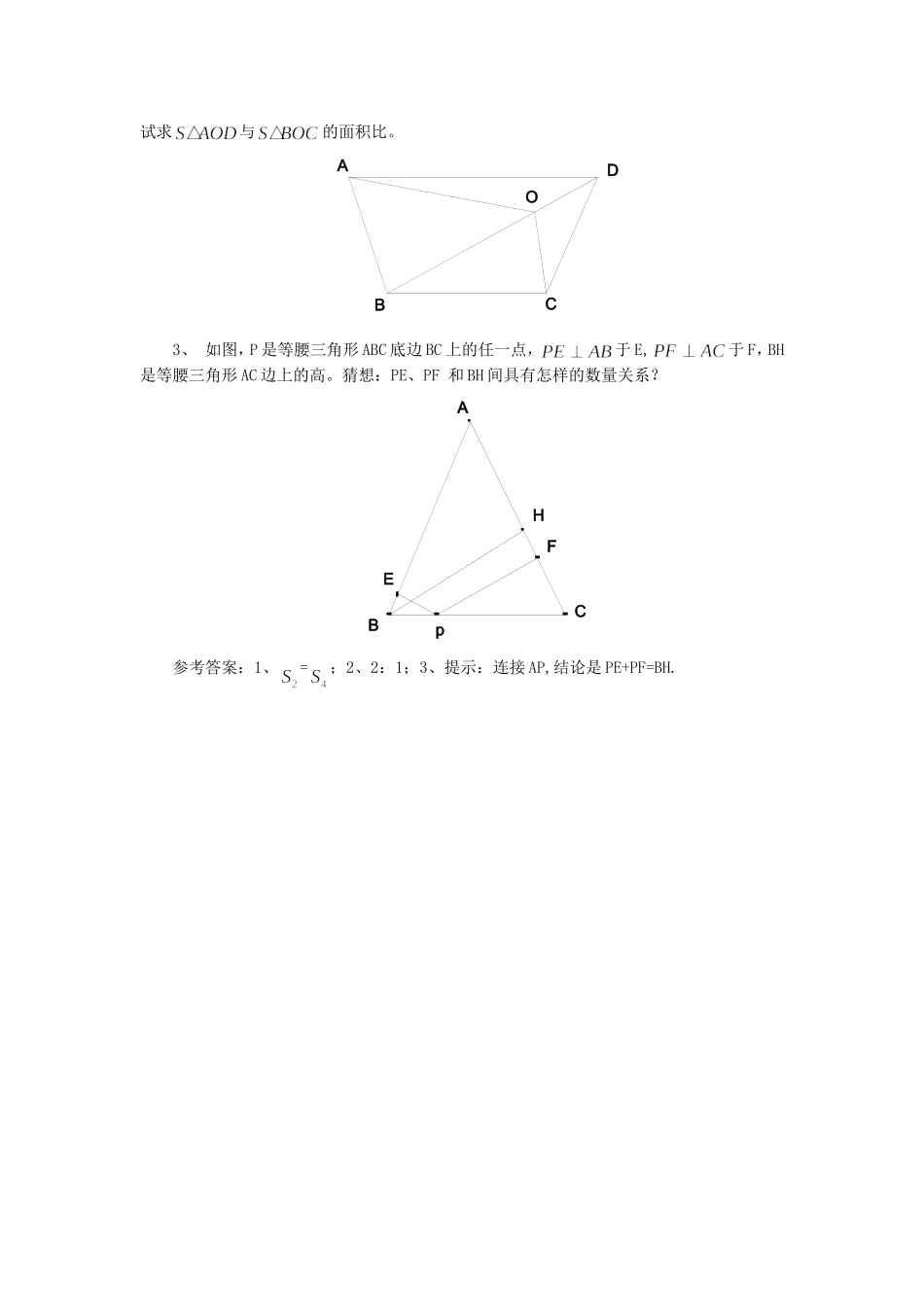
在三角形中巧用面积法解题所谓面积法是指借助图形面积自身相等的性质、可拆分的性质和可比的性质进行解题的一种方法。在中学阶段它是数学中一种常用的解题方法。并且具有解题便捷快速、简单易懂等特点。现分类举例如下,希望同学们在今后的做题中有所启发。一、利用面积自身相等的性质解题例1如图,在直角三角形ABC中,AB=13,AC=12,BC=5,求AB边上的高AD的长。解析:因为S=AB×CD,又S=AC×BC,所以AB×CD=AC×BC,即13×CD=12×5,得CD=。例2在中,AB>AC,BD、CE分别是AC、AB边上的高,试判断BF和CE的大小关系,并说明理由。解析:由S=S,所以AB×CE=AC×BF,而AB>AC,所以BF>CE。小结:利用一个图形面积自身相等的性质解题,就是从不同的角度使用面积公式来表示同一个图形的面积,列出等式求出未知的量。二、利用面积的可比性解题例3如图,由图中已知的小三角形的面积的数据,可得的面积为。解析:由图可得,,又与具有公共顶点,且等高不等底,所以,又知,,所以,得=120,所以的面积为90+120=210。小结:我们知道等底等高的两三角形的面积相等,等底不等高的两三角形面积的比等于其对应高的比,等高而不等底的两三角形面积的比等于其对应底的比。三、利用面积的可分性解题例4如图,已知等边三角ABC,P为内一点,过P作的高为h.试说明。ABCDPFE解析:连接PA、PB、PC,由题意得,所以,又因为AB=AC=BC,所以。小结:用面积的可分性解题,一般要将图形分成若干个小三角形,利用其整体等于部分之和建立关于条件和结论的关系式,从而方便快捷地解决问题。现提供部分习题供同学们练习:1、如图,已知和,AC与BD交于点o,且直线AD∥BC,图中四个小三角形的面积分别为、、、,试判断和的大小关系,并说明理由。DBAOCS4S3S1S22、如图,四边形ABCD中,对角线BD上有一点O,OB:OD=3:2,=6,=1,试求与的面积比。DACBO3、如图,P是等腰三角形ABC底边BC上的任一点,于E,于F,BH是等腰三角形AC边上的高。猜想:PE、PF和BH间具有怎样的数量关系?ABCpEFH参考答案:1、=;2、2:1;3、提示:连接AP,结论是PE+PF=BH.