绝对值不等式的解法VIP免费

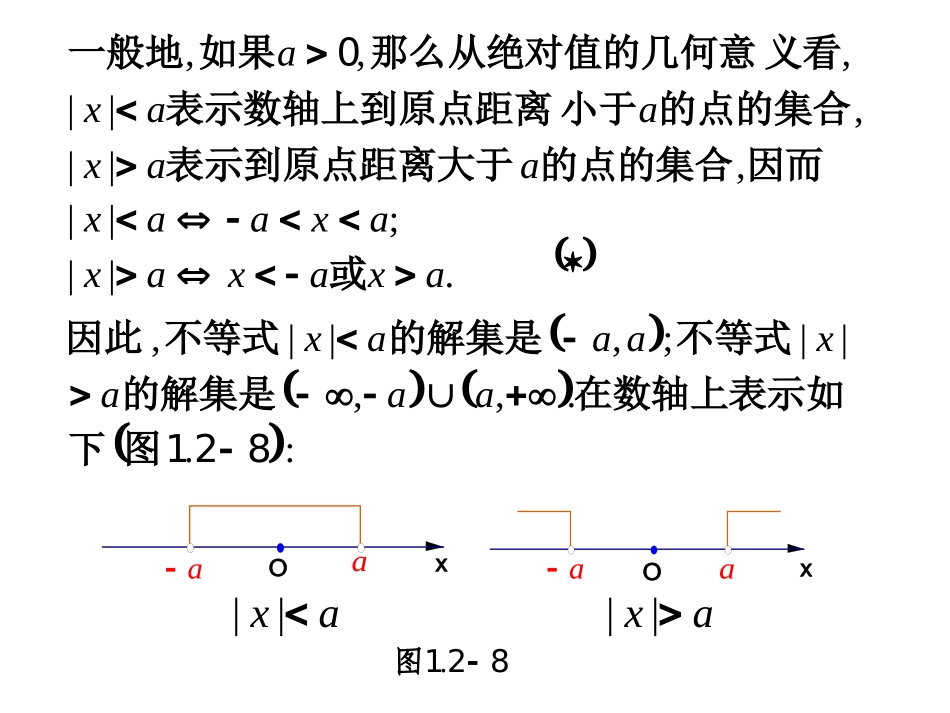
2绝对值不等式的解法主备：冯宗明喻浩徐洪燕审核：牟必继古之立大事者，不惟有超世之材，亦必有坚忍不拨之志.,,,,,||;,,,,||,11111111即的点的集合数轴上到原点距离大于它的解集是由绝对值的几何意义对于不等式即的点的集合小于点距离它的解集是数轴上到原几何意义由绝对值的对于不等式我们知道xx.||;||,||,||,,,axaxaxaxaaxaaxaaxa或因而的点的集合表示到原点距离大于的点的集合小于表示数轴上到原点距离义看那么从绝对值的几何意如果一般地0:..,,||;,||,821图下在数轴上表示如的解集是不等式的解集是不等式因此aaaxaaaxaaOxax||aaOax||x821.图我们有或对于绝对值不等式是一个正实数例如等式而得到上述不解一般可以通过转化为即其他绝对值不等式的的基础是解其他绝对值不等式上述绝对值不等式,)||(||,,.,,axxaxxa11;||axxaxaxxaaxx1111axxaxxaxx111或,||.,axxaxx11或921.图ax1ax11xxaxx||1x1xaxx||1ax1ax1..,,,||所示如图可以在数轴上表示出来以上不等式的解所以的点的距离的点与坐标为标为的几何意义是数轴上坐由于绝对值92111xxxx.,的不等式可以解一些含有绝对值式及绝对值的几何意义利用上述型不等式的解法和cbaxcbax||||1.||2133x解不等式例,,||2132213xx得由解得解,131x.,131xx原不等式的解集为因此..,,,||,所示如图合的点的集离不大于的点的距标为它的解集是数轴上到坐得两边除以如果将从几何上看1021323132313213xxOx313111021.图.||7324x解不式例,||||723732xx得由解,,723723xx或所以,335xx或从而.335xxx或所以原不等式的解集为?解的几何解释吗等式的你能给出上述绝对值不探究等式的解法型不和cbxaxcbxax||||||||2.||||5215xx解不等式例.,,.,,,,,..,就可以得出不等式的解位置出具有上述特点的点的我们只要在数轴上确定所以的点所对应的实数点的距离之和不小于两轴上到那么不等式的解就是数别是对应的点分数轴上与设如图意义来分析我们从它的几何比较复杂这个绝对值不等式分析5121121BABAxO1AAB1B3-2-1-121121.图xO1AAB1B3-2-1-121121.图.,,,,,,.的解上的数都不是原不等式因此区间是两点的距离那么为对应的点分别轴上与设数如图解法一123121121BABA;||||,.,,515111BAAAAABA这时有位到点个单向左移动将点的点的距离之和为点关键要在数轴上找出与为了求出不等式的解;||||,,51111BBABBB这时也有个单位到点向右移动将点同理的的左边或点点的距离之和都小于点之间的任何点到与点点从数轴上可以看到11115BABABA;,,xO1AAB1B3-2-1-121121.图.,5离之和都大于的距右边的任何点到BA.,,,23原不等式的解集是所以.,,,,,,,,,,||||,,等式的解集们综合在一起就得到不它把后然况的情解的三个区间上讨论不等式分别在这先了三个区间集分成实数把对应的点数轴上与时解可以发现解法述上分析112212521BAxx..,,,,,因此我们有如下解法绝对值的不等式为不含绝对值不等式可以转化在这三个区间上将数轴分为三个区间为分界点以点事实上BA,,,35212xxxx解得原不等式可以化为时当解法二5212||||,xxx即不等式组.,3的解集是.,,,矛盾即原不等式可以化为时当5352112xxx52112||||,xxx所以不等式组.的解集为,,,25211xxxx解得原不等式可以化为时当5211||||,xxx即不等式组.,2的解集是.,,,23原不等到的解集是综上所述.,,.,,的解集利用函数图象求不等式数的观点我们也可以从函类似地根近似图象求方程的可以利用函数的关系的根零点与方程的由函数时我们知道在学习函数知识0xfxfy321121...