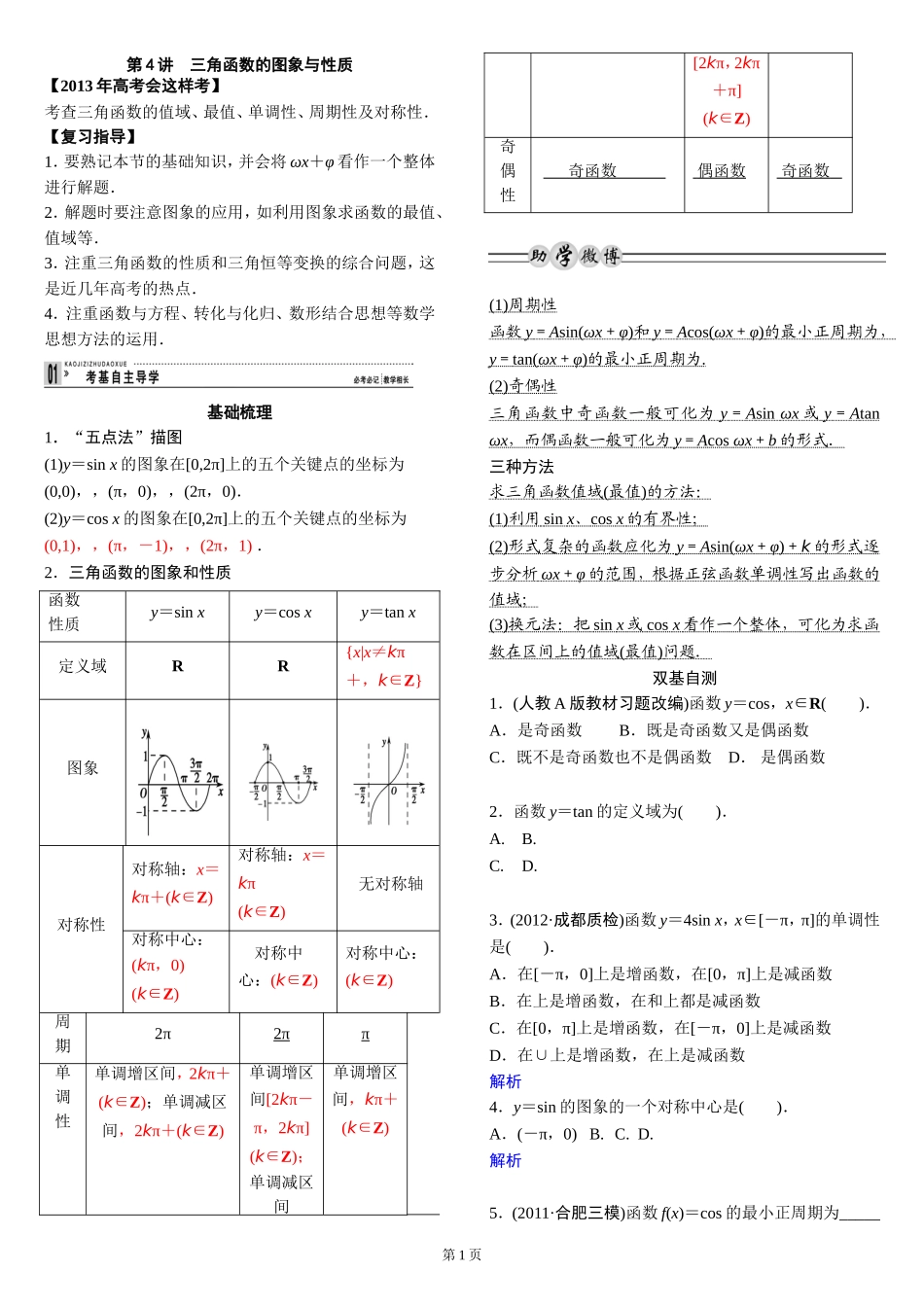
第4讲三角函数的图象与性质【2013年高考会这样考】考查三角函数的值域、最值、单调性、周期性及对称性.【复习指导】1.要熟记本节的基础知识,并会将ωx+φ看作一个整体进行解题.2.解题时要注意图象的应用,如利用图象求函数的最值、值域等.3.注重三角函数的性质和三角恒等变换的综合问题,这是近几年高考的热点.4.注重函数与方程、转化与化归、数形结合思想等数学思想方法的运用.基础梳理1.“五点法”描图(1)y=sinx的图象在[0,2π]上的五个关键点的坐标为(0,0),,(π,0),,(2π,0).(2)y=cosx的图象在[0,2π]上的五个关键点的坐标为(0,1),,(π,-1),,(2π,1).2.三角函数的图象和性质函数性质y=sinxy=cosxy=tanx定义域RR{x|x≠kπ+,k∈Z}图象对称性对称轴:x=kπ+(k∈Z)对称轴:x=kπ(k∈Z)无对称轴对称中心:(kπ,0)(k∈Z)对称中心:(k∈Z)对称中心:(k∈Z)周期2π2ππ单调性单调增区间,2kπ+(k∈Z);单调减区间,2kπ+(k∈Z)单调增区间[2kπ-π,2kπ](k∈Z);单调减区间单调增区间,kπ+(k∈Z)[2kπ,2kπ+π](k∈Z)奇偶性奇函数偶函数奇函数(1)周期性函数y=Asin(ωx+φ)和y=Acos(ωx+φ)的最小正周期为,y=tan(ωx+φ)的最小正周期为.(2)奇偶性三角函数中奇函数一般可化为y=Asinωx或y=Atanωx,而偶函数一般可化为y=Acosωx+b的形式.三种方法求三角函数值域(最值)的方法:(1)利用sinx、cosx的有界性;(2)形式复杂的函数应化为y=Asin(ωx+φ)+k的形式逐步分析ωx+φ的范围,根据正弦函数单调性写出函数的值域;(3)换元法:把sinx或cosx看作一个整体,可化为求函数在区间上的值域(最值)问题.双基自测1.(人教A版教材习题改编)函数y=cos,x∈R().A.是奇函数B.既是奇函数又是偶函数C.既不是奇函数也不是偶函数D.是偶函数2.函数y=tan的定义域为().A.B.C.D.3.(2012·成都质检)函数y=4sinx,x∈[-π,π]的单调性是().A.在[-π,0]上是增函数,在[0,π]上是减函数B.在上是增函数,在和上都是减函数C.在[0,π]上是增函数,在[-π,0]上是减函数D.在∪上是增函数,在上是减函数解析4.y=sin的图象的一个对称中心是().A.(-π,0)B.C.D.解析5.(2011·合肥三模)函数f(x)=cos的最小正周期为_____第1页___.答案π考向一三角函数的定义域与值域【例1】►(1)求函数y=lgsin2x+的定义域.(2)求函数y=cos2x+sinx的最大值与最小值.[审题视点](1)由题干知对数的真数大于0,被开方数大于等于零,再利用单位圆或图象求x的范围.(2)将余弦化为正弦,再换元处理,转化为关于新元的一元二次函数解决.解【方法总结】(1)求三角函数的定义域实际上是解简单的三角不等式,常借助三角函数线或三角函数图象来求解.(2)求解三角函数的值域(最值)常见到以下几种类型的题目:①形如y=asinx+bcosx+c的三角函数化为y=Asin(ωx+φ)+k的形式,再求最值(值域);②形如y=asin2x+bsinx+c的三角函数,可先设sinx=t,化为关于t的二次函数求值域(最值);③形如y=asinxcosx+b(sinx±cosx)+c的三角函数,可先设t=sinx±cosx,化为关于t的二次函数求值域(最值).【训练1】(1)求函数y=的定义域.(2)已知函数f(x)=cos+2sin·sin,求函数f(x)在区间上的最大值与最小值.解考向二三角函数的奇偶性与周期性【例2】►(2011·大同模拟)函数y=2cos2-1是().A.最小正周期为π的奇函数B.最小正周期为π的偶函数C.最小正周期为的奇函数D.最小正周期为的偶函数[审题视点]先化简为一个角的三角函数,再确定周期和奇偶性.解析【方法总结】求解三角函数的奇偶性和周期性时,一般先要进行三角恒等变换,把三角函数式化为一个角的一个三角函数,再根据函数奇偶性的概念、三角函数奇偶性规律、三角函数的周期求解公式进行.【训练2】已知函数f(x)=(sinx-cosx)sinx,x∈R,则f(x)的最小正周期是________.解析考向三三角函数的单调性【例3】►已知f(x)=sinx+sin,x∈[0,π],求f(x)的单调递增区间.[审题视点]化为形如f(x)=Asin(x+φ)的形式,再求单调区间.解第2页.【方法总结】求形如y=Asin(ωx+φ)+k的单调区间...